5.2 Örnek DFA Uygulamaları ve Sonuçların Yorumlanması
DFA, R üzerinde “lavaan” (Rosseel, 2012) paketi yardımıyla kolayca hesaplanabilir. Bunun için öncelikle lavaan paketinin install.packages("lavaan) komutu ile yüklenmesi gerekmektedir. “lavaan”, Yves Rosseell tarafından gizil değişken modellemesinde kullanılmak üzere geliştirilmekte olan özgür bir yazılımdır. “lavaan”ın kendine has bir syntax yapısı bulunsa da oldukça kolay kurallar tanımlanmıştır. Örneğin; a1, a2, a3 maddeleri Faktör A altında toplanırken, b1, b2 ve b3 maddelerinin Faktör B altında toplandığını varsayalım. “a” maddelerinin gerçekten de Faktör A ve “b” maddelerinin gerçekten de Faktör B altında yer alıp almadığını test etmede kullanılacak basit bir lavaan modeli aşağıdaki gibi kurulabilir:
model <- "Faktor_A =~ a1 + a2 + a3
Faktor_B =~ b1 + b2 + b3"
dfa <- sem(model = model, data = veri, estimator = "MLR")Bu söz diziminde (sintaks) öncelikle test edilecek model tek tırnak arasında tanımlanmaktadır. Faktör A’yı oluşturan maddeleri ifade etmek için gizil ve gözlenen değişkenler arasında =~ operatörü kullanılmaktadır. Daha sonra gözlenen değişkenler arasında ise + operatörü kullanılır. DFA’nın gerçekleştirilmesi içinse lavaan paketi içerisinde yer alan **sem** fonksiyonu kullanılır.
Bu fonksiyonun ilk parametresinde test edilecek olan model belirtilir. Daha sonra modelin hangi veri seti ile test edileceği ve ardından kullanılacak olan parametre kestirim yönteminin belirtilmesi gerekmektedir. Yukarıdaki örnekte kestirim yöntemi olarak Robust Maximum Likelihood yöntemi seçilmiştir. estimator argümanının belirtilmemesi halinde varsayılan olarak “ML” yöntemi kullanılacaktır. Ayrıca “MLR” yerine “ULS”, “WLS” ve “DWLS” yazılarak kestirim yöntemi değiştirilebilir.
5.2.1 Test Sonuçlarının Yorumlanması
Yukarıdaki örnekte yer alan kod çalıştırıldığında, “dfa” adlı bir nesne oluşacaktır. Bu bir “lavaan” nesnesidir ve içinde tüm doğrulayıcı faktör analizi sonuçlarını tutar. Bu nesne kullanarak analiz hakkında istenilen bilgiler elde edilebilir. Bunun için aşağıdaki koddan yararlanılması mümkündür:
## lavaan 0.6.15 ended normally after 27 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 13
##
## Number of observations 252
##
## Model Test User Model:
## Standard Scaled
## Test Statistic 72.331 66.370
## Degrees of freedom 8 8
## P-value (Chi-square) 0.000 0.000
## Scaling correction factor 1.090
## Yuan-Bentler correction (Mplus variant)
##
## Parameter Estimates:
##
## Standard errors Sandwich
## Information bread Observed
## Observed information based on Hessian
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Faktor_A =~
## a1 1.000 0.574 0.521
## a2 1.397 0.311 4.488 0.000 0.802 0.735
## a3 1.426 0.297 4.807 0.000 0.819 0.746
## Faktor_B =~
## b1 1.000 0.465 0.449
## b2 1.276 0.220 5.797 0.000 0.593 0.563
## b3 1.791 0.425 4.216 0.000 0.833 0.766
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Faktor_A ~~
## Faktor_B 0.232 0.086 2.704 0.007 0.870 0.870
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .a1 0.888 0.106 8.334 0.000 0.888 0.729
## .a2 0.548 0.114 4.789 0.000 0.548 0.460
## .a3 0.533 0.120 4.456 0.000 0.533 0.443
## .b1 0.859 0.094 9.176 0.000 0.859 0.799
## .b2 0.759 0.116 6.522 0.000 0.759 0.683
## .b3 0.489 0.096 5.114 0.000 0.489 0.413
## Faktor_A 0.330 0.112 2.941 0.003 1.000 1.000
## Faktor_B 0.216 0.090 2.410 0.016 1.000 1.000Çıktının ilk satırındaki uyarı kullanılan paket olan lavaan’a ait sürüm numarasını ve analizin kaç iterasyonun ardından sonlandığını bildirmektedir. Ardından hangi kestirim yönteminin kullanıldığı raporlanmaktadır. MLR yöntemi temelde ML’a dayandığı için bu satırda ML görünmektedir. Ancak çıktının ilerleyen satırlarında Robust sütunu görülebilir.
Parametre ve gözlem sayılarına yer verildikten sonra modele ait ki-kare istatistiği, serbestlik derecesi ve p değeri görülmektedir. Bu değerler modelin uyum iyiliğini değerlendirmede kullanıldığı için Uyum iyiliği başlığında yorumlanmıştır.
Ardından her bir gizil değişken ve gözlenen değişken arasındaki regresyon eşitlikleri raporlanmaktadır. Burada dikkat edilirse her bir gizil değişkenin yani faktörün ilk maddesine ait kestirim 1.000 olarak görünmekte, standart hata, “z” ve “p” değerleri ise boş olarak raporlanmaktadır. Bunun nedeni birden fazla gizil değişken bulunduğunda, her bir gizil değişkenin ölçeklenmesi gerekliliğidir. Herhangi bir ek komut girilmediğinde, her bir gizil değişkene ait birinci gözlenen değişkenin faktör yükü 1.00 kabul edilerek ölçekleme yapılır. “std.lv” argümanı eklenip değeri TRUE olarak belirtildiğinde ise gizil değişkenin varyansı 1.00 olacak şekilde bir ölçekleme yapılır.
Estimate sütununda, standartlaştırılmamış faktör yükleri yer alır. Bu yükler birer standartlaştırılmamış regresyon katsayısı olarak yorumlanmaktadır. Örneğin a3 maddesine ait standartlaştırılmamış faktör yükü 1.426 olarak bulunmuştur. Bunun anlamı, A faktörü ile ölçülen yapıdaki 1 birimlik artış, a3 maddesinde 1.426 birimlik bir artışla ilişkilidir. “std.all” sütununda ise tamamen standartlaştırılmış faktör yükleri yer almaktadır. Standartlaştırılmış faktör yükleri, hem gizil hem de gözlenen değişkenlerin ortalaması 0 ve standart sapması 1 olan standart bir dağılıma göre ölçeklenmesi sonucu elde edilir. Yani A faktörü ile ölçülen yapıdaki 1 standart sapmalık artış, a3 maddesindeki 0.746 standart sapmalık bir artışla ilişkilidir. Bunun yanında binişik madde yoksa, yani her bir gözlenen değişken yalnızca tek bir gizil değişken ile ilişkiliyse standartlaştırılmış faktör yükleri birer korelasyon katsayısı olarak da yorumlanabilir. Bu değerin karesi hesaplandığında ise faktör ile madde varyansının yüzde kaçının açıklandığı yorumlanabilir. a3 maddesi için standart faktör yükünün karesi 0.746^2 = 0.557’dir. Yani A faktörü ile a3 maddesindeki varyansın %55.7’si açıklanabilmektedir. Başka bir deyişle a3 maddesindeki gözlenen varyansın %44.3’ü maddeye ait biricik varyans ya da hata varyansıdır.
Aynı tablodaki “std.lv” sütunu ise yalnızca ilgili gizil faktör dikkate alınarak hesaplanan standartlaştırılmış faktör yüklerini temsil etmektedir.
“Std.Err”, standartlaştırılmamış faktör yüküne ait standart hata değeriyken, “z-value” bu değere ait z istatistiğini ve “P(>|z|)” ise hesaplanan z istatistiğine ait “p” değerini vermektedir. “p” değerinin, araştırmacı tarafından kabul edilen alfa düzeyinden (ör: .05) küçük olması, faktörün bu maddeyi açıklamada anlamlı bir rolü olduğunu göstermektedir.
5.2.1.1 Uyum iyiliği
Bir önceki başlıkta modelde yer alan gözlenen ve gizil değişkenler arasındaki ilişkinin nasıl yorumlandığı gösterilmişti. Ancak DFA sonuçlarının yorumlanmasında DFA modelinin bir bütün olarak veri ile ne derecede uyum gösterdiğinin de incelenmesi gerekir. Bunun için uyum iyiliği indislerinden (goodness of fit indices) yararlanılmaktadır. Bu indisleri elde etmek için yukarıda belirtilen fonksiyonda bir parametre tanımlaması yapılması yeterlidir:
Yukarıdaki kod, bir lavaan nesnesi olan dfa’nın sonuçlarını, standartlaştırılmış faktör yükleri ve uyum iyiliği indeksleriyle birlikte uyum adında bir nesneye kaydetmektedir. Bu işlemin sonucunda uyum içerisinde iki adet öge barındıran bir liste olarak kaydedilir. Bu bölümdeki R çıktılarında tekrarı önlemek adına yalnızca uyum iyiliği indeksleri aşağıdaki kod ile çağrılmıştır. Normal şartlarda yukarıdaki kodu çalıştırdığınızda tüm DFA sonuçlarını görebilirsiniz. Ancak yalnızca uyum iyiliği indekslerini görmek için aşağıdaki kodun çalıştırılması gerekir:
## NULLÇıktıda görülebileceği üzere birtakım katsayılar verilmiştir. Bu katsayıların birçoğu modelin veri ile olan uyumunu yorumlamada kullanılır.
Dikkat edilirse bu kısımdaki değerlerden bazılarının sonunda robust eki bulunmaktadır. Analizin yapılmasında ML yerine MLR tercih edildiği için robust ile işaretlenmiş değerlerin yorumlanması gerekmektedir. Alanyazında yorumlanan birçok uyum iyiliği indeksi bulunmaktadır. Verinin modelle uyumunu yorumlarken bu indekslerden yalnızca biri ile çalışılmaz, birden çok indeks bir arada yorumlanır.
En sık kullanılan indekslerden biri \({\chi}^2 / sd\) değeridir. \({\chi}^2\) istatistiği örneklem büyüklüğünden kolayca etkilenebildiği için serbestlik derecesine bölünmektedir. Ancak bu bölümün başında belirtildiği gibi DFA modellerinde serbestlik derecesi örneklem büyüklüğüne değil maddedeki parametre sayısına bağlıdır. Dolayısıyla \({\chi}^2\)’yi serbestlik derecesine bölmek örneklem büyüklüğünün etkisini azaltmamaktadır. Bu nedenle de geniş örneklem büyüklüklerinde \({\chi}^2 / sd\) model uyumunun hatalı yorumlanmasına yol açabilir. Tabachnick ve Fidell (2001) \({\chi}^2 / sd {\leq} 2\); Kline (2011) \({\chi}^2 / sd {\leq} 3\) ve Wheaton ve diğerleri (1977) \({\chi}^2 / sd {\leq} 5\) ölçütlerini model uyumunun göstergesi olarak yorumlanmaktadır. Bu kısımda verilen ve verilecek olan ölçütler, sırasıyla mükemmel uyum, iyi uyum ve kabul edilebilir uyum göstergeleri olarak yorumlanabilir.
Sık kullanılan bir diğer uyum iyiliği indeksi ise RMSEA’dır. RMSEA değerinin ise 0’a yakın olması gerekmektedir. Bu bağlamda Hooper, Coughlan ve Mullen (2008) \(RMSEA {\leq} .03\), Jöreskog ve Sorbom (1993) ise sırasıyla \(RMSEA {\leq} .05\) ve \(RMSEA {\leq} .08\) ölçütlerinin kullanılabileceğini ifade etmiştir.
Ortalama hataların karekökünü veren RMR ve Standartlaştırılmış RMR (SRMR)’nin ise Tabachnick ve Fidell (2001) 0’a yakın olmasının mükemmel uyuma işaret ettiğini ifade etmiştir. Kline (2011) ise \(SRMR {\leq} .05\) ve Anderson ve Gerbing (1984) \(RMSEA {\leq} .08\) ölçütlerini kullanmıştır.
CFI (Comperative fit index) ve TLI (NNFI) ise Normed Fit Indexten (NFI) türetilmiş ve NFI’nın örnekleme bağlılığını azaltan çözümler sunmuş iki uyum indeksidir. Her iki indeks de benzer ölçütlere göre yorumlanır ve değerlerin 1’e yakın olması modelin veri ile uyum gösterdiği anlamına gelir. Kline (2011) \(CFI {\geq} .90\), Hu ve Bentler (1999) \(CFI {\geq} .95\) değerlerini ölçüt olarak önermiştir.
GFI (Goodnes of fit index) ve AGFI (Adjusted goodnes of fit index) indeksleri de model uyumunun yorumlanmasında kullanılsa da örneklem büyüklüğünden etkilenmesi nedeniyle son zamanlarda raporlamada tercih edilmeyen indekslerdir.
5.2.2 “SemPlot” Paketi ile Grafiksel Gösterim
DFA bulgularının yorumlanmasını kolaylaştırmak için test edilen modelin görsel olarak temsil edilmesi önemlidir. Bu amaçla yol grafiklerinden yararlanılır. Birçok yazılım DFA yapıldığı sırada bu yol grafiğini otomatik olarak oluşturmaktadır. R’da ise bunu yapmak için yardımcı bir paket olan semPlot’tan yararlanılabilmektedir. Yukarıda test edilen modele ait yol grafiği aşağıda verilmiştir:
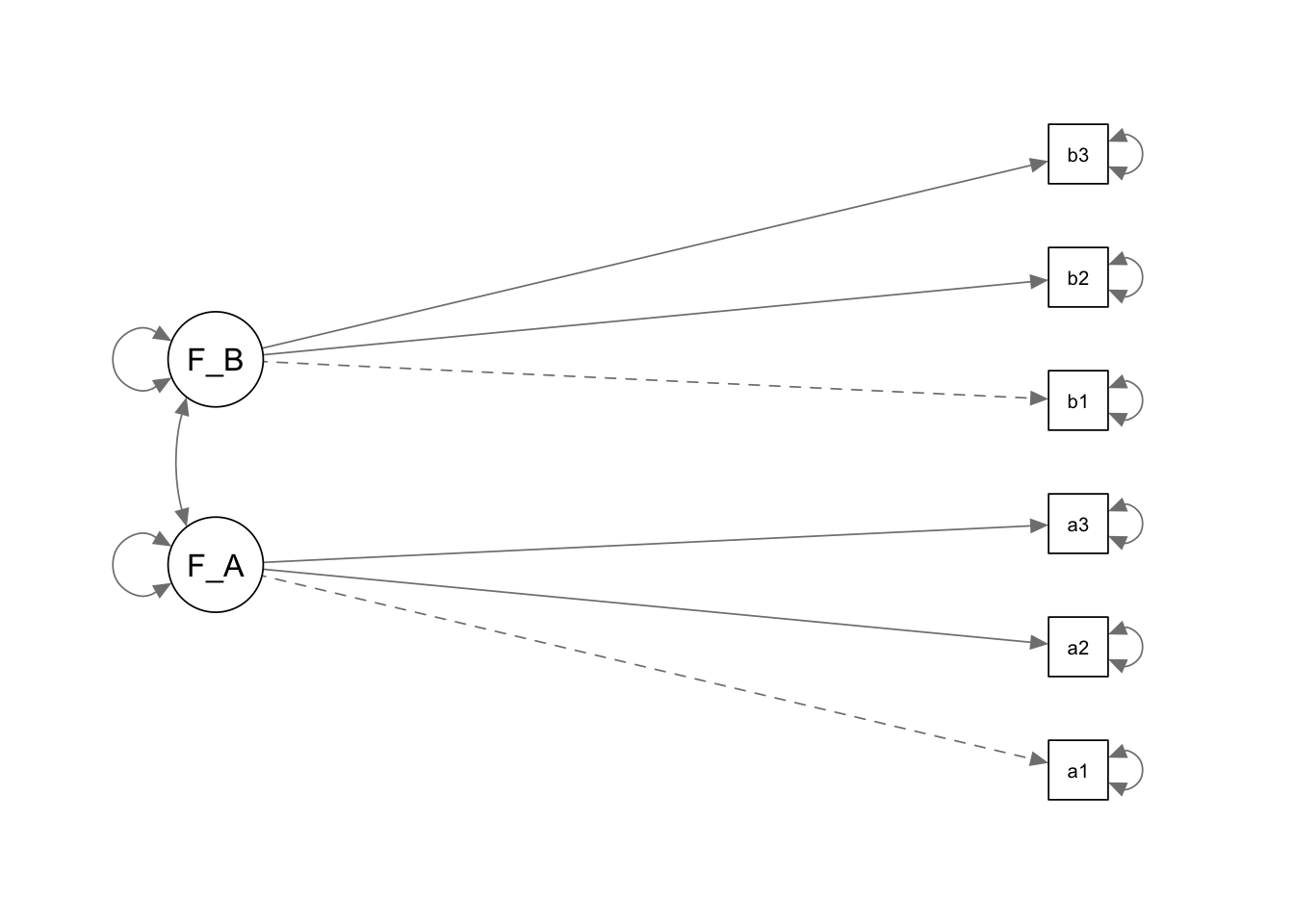
semPaths fonksiyonuna ait argümanlar incelendiğinde, ilk argüman olarak grafiği elde edilecek “lavaan” nesnesinin adının girildiği görülmektedir. “what” argümanı, hangi özelliğe ait yol grafiğinin elde edileceğini göstermektedir. Bu kısma örnekteki gibi “paths” yazılması halinde, yalnızca model çizilecek, herhangi bir katsayı gösterilmeyecektir. “est” tanımlaması yapıldığında, standartlaştırılmamış faktör yükleri; “std” tanımlaması yapıldığında ise standartlaştırılmamış faktör yükleri grafik üzerinde raporlanacaktır. “layout” argümanı grafikteki öğelerin nasıl düzenleneceğini ayarlar. Bu argümana “tree”, “circle”, “tree2”, “circle2” ve “spring” seçenekler yazılabilir. “rotation” ise grafiğin nasıl döndürüleceğini ayarlar ve 1, 2, 3, 4 seçeneklerini alabilir.
5.2.3 Modifikasyonlar
Model uyumunun daha iyi hale getirilmesinde modifikasyon indekslerinden yararlanılmaktadır. Ancak modifikasyonlar tamamen matematiksel önerilerdir. Kuramsal altyapısı olmadan modelde modifikasyon yapma yolu tercih edilmemelidir. R tarafından iki çeşit modifikasyon önerilmektedir, bunlar “gözlenen ve gizil değişken arasındaki modifikasyonlar” ve “değişkenler arası hata varyanslarının ilişkilendirilmesine yönelik modifikasyonlar”dır. Bir maddenin, başka bir faktör altına alınması genellikle kuramsal olarak temellendirilemeyecek bir modifikasyondur. Dolayısıyla DFA yapılan çalışmalar incelendiğinde bu gibi modifikasyonların yapıldığına çok rastlanmaz. Öte yandan hata varyanslarının ilişkilendirilmesi kuramsal olarak daha açıklanabilir bir modifikasyondur. Bölümün başında, hata varyansının aslında ölçme sonuçlarına karışan hata olmadığını, diğer maddelerle paylaşılan ortak varyans dışında kalan varyansı temsil ettiği ifade edilmişti. Dolayısıyla aynı faktör altında yer alan, benzer ifadeleri içeren maddelerin diğer maddelerle paylaşmadıkları bu varyansın ilişkili hale getirilmesi açıklanabilir bir durumdur.
Yazılım tarafından önerilen modifikasyonların görülebilmesi için aşağıdaki kod çalıştırılır.
## lhs op rhs mi epc sepc.lv sepc.all sepc.nox
## 34 b1 ~~ b2 23.504 0.285 0.285 0.353 0.353
## 18 Faktor_A =~ b3 23.504 5.351 3.074 2.826 2.826
## 24 a1 ~~ b1 20.463 0.272 0.272 0.311 0.311
## 27 a2 ~~ a3 16.765 0.367 0.367 0.680 0.680
## 19 Faktor_B =~ a1 16.765 2.469 1.149 1.041 1.041
## 25 a1 ~~ b2 16.412 0.238 0.238 0.290 0.290
## 17 Faktor_A =~ b2 12.860 -2.299 -1.321 -1.253 -1.253
## 35 b1 ~~ b3 12.859 -0.241 -0.241 -0.372 -0.372
## 29 a2 ~~ b2 11.809 -0.191 -0.191 -0.296 -0.296
## 22 a1 ~~ a2 11.791 -0.213 -0.213 -0.306 -0.306
## 21 Faktor_B =~ a3 11.790 -2.912 -1.355 -1.235 -1.235Bu kod, daha önce oluşturulan dfa nesnesi için modifikasyon indekslerini verecektir. Fonksiyon içerisindeki “sort.” argümanının “TRUE” olması, modifikasyon indeksini büyükten küçüğe sıralamakta, “minimum.value” argümanı ise atanan değerin altındaki indeksleri göstermemeyi sağlamaktadır. Örnek incelendiğinde b1 ve b2 maddelerinin hata varyanslarının ilişkilendirilmesi halinde model uyumunun artacağı görülmektedir. İkinci modifikasyon önerisinde ise b3 maddesinin Faktor_B yerine Faktor_A altına alınmasının modeli daha uyumlu hale getireceği belirtilmektedir. Ancak bu ikinci modifikasyonu yapabilmek için güçlü kuramsal kanıtlara ihtiyaç vardır. Bu nedenle b1 ve b2 maddelerine ait hata varyanslarının ilişkilendirilmesi, bu maddelerin aynı faktör altında yer alması ve ifadelerindeki olası benzerlikler de göz önüne alınarak, açıklanabilir.
Bu modifikasyonun gerçekleştirilmesi için DFA’nın test edildiği modelde bir değişiklik yapılması ve ardından modelin tekrar test edilmesi gerekmektedir. Bu işlem aşağıdaki kodla yapılabilir:
Dikkat edilirse modelde b1 ve b2 maddelerinin hatalarını ilişkilendirmek için ~~ operatörü kullanıldı. Bu operatör aynı zamanda modifikasyon indekslerinin çıktısında bu maddeler arasında da gösterilen operatördür.
Model tanımlaması yapıldıktan sonra DFA tekrar hesaplanır:
dfa <- sem(model = model, data = veri, estimator = "MLR")
uyum <- summary(dfa, standardized = TRUE, fit.measures = TRUE)## NULLÇıktılardaki uyum indeksleri incelendiğinde modelin veri ile daha uyumlu hale geldiği anlaşılmaktadır. Örneğin CFI değeri .789’dan .897’ye çıkmıştır. Ancak yukarıdaki bazı indislerinin halen uygun düzeyde olmadığı görülmektedir. Bu durumda, uygunsa, modifikasyon yapmaya devam edebilir ya da alternatif modeller üzerinde çalışılabilir.