2.1 Klasik Test Kuramı ve Kavramsal Çerçevesi
Gerçek puan teorisi olarak da adlandırılan klasik test kuramı (KTK) özünde ölçme sonuçlarını anlamak, düzenlemek ve yorumlamak için kullanılan bir ölçme yapısıdır (Desjardins & Bulut, 2018). KTK bakış açısına göre her gözlem veya ölçme işlemi belirli miktarda hata içerir. Bu bağlamda bir ölçme aracı ile elde edilen ölçme sonucu gerçek puan (T), gözlenen puan (X) ve hata olmak üzere üç bileşenle ifade edilebilir. KTK’nın matematiksel gösterimi aşağıdaki gibi ifade edilebilir.
KTK Matematiksel Model

Bu modelde “X” gözlenen ölçme sonucunu veya eğitim alanı bağlamında ele alırsak test puanını ifade eder. “E” sembolü ölçme sürecinde karışan rastgele (seçkisiz) hataları içerir. “T” sembolü ise gerçek puanı ifade eder. Bu bağlamda gözlenen puan rastgele hata ve gerçek puan olmak üzere iki bileşenden oluşur. Ölçme sürecine sabit, sistematik ve rastgele (seçkisiz) olmak üzere üç tür hata karışmaktadır. KTK bu üç hata türünden rastgele hataya odaklanır. Güvenirlik test puanlarının rastgele hatalardan arınıklık düzeyi olarak tanımlanabilir. Bu bağlamda KTK güvenirlik kavramı üzerinde odaklanan bir kuramdır. Diğer bir ifade ile güvenirlik tekrarlanan ölçüm sonuçlarının benzeşikliği üzerine kuruludur. Ancak psikolojik özelliklerin ölçümü söz konusu olduğunda, çok sayıda tekrarlı ölçüm elde edilmesi pratik anlamda mümkün olmamaktadır. Bu nedenle KTK tekrarlı ölçümlerden ziyade paralel ölçmelere odaklanır. Diğer bir ifadeyle güvenirlik iki paralel form arasındaki korelasyon katsayısı olarak da ifade edilebilir (Baykul, 2000).
Bunlara ek olarak klasik test kuramı üç temel varsayıma dayanır.
1- Gözlenen değerlerin beklenen değeri (aritmetik ortalaması) gerçek puanı verecektir.
2- Gerçek puanlar ve hatalar birbirinden bağımsızdır. Diğer bir ifade ile gerçek puan ve rastgele hata arasındaki ilişki sıfıra eşittir.
3- Farklı test formları arasındaki hatalar birbirlerinden bağımsızdır. (Magnusson, 1968 akt Erkuş vd. 2020)
Bu üç sayıltıyı biraz daha detaylı açıklayalım. Birinci varsayım için ölçme sürecinde karışan rastgele hatalar bazen pozitif bazen de negatif yönde olabileceği için bu hataların ortalaması sıfır olacaktır. İkinci varsayım bağlamında yüksek gerçek puana sahip kişilerin ölçme sonucuna daha fazla hata karışması veya bunun tam tersinin olması söz konusu değildir. Başka bir ifade ile rastgele (seçkisiz) dağılan hatalar, gerçek puan dağılımı ile korelasyon göstermez. Aksi durumda hatanın seçkisiz değil sistematik olması gerekir. Üçüncü varsayıma bakıldığında ise az önce belirtildiği gibi iki seçkisiz dağılımın korelasyon göstermesi mümkün değildir. Paralel formlar için de hata seçkisiz dağılacağı için iki ya da daha fazla paralel formun hataları arasında bir korelasyon olması beklenmez.
Belirtilen varsayımlara dayalı olarak KTK matematiksel modeli aşağıdaki gibi yeniden ifade edilebilir.
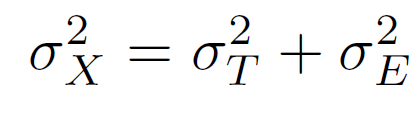
Buna göre gözlenen puan varyansı gerçek puan varyansı ile hata varyansının toplamından elde edilir. Bu bağlamda gerçek puan varyansı sabit kabul edilirken hata varyansı çeşitli etmenlere dayalı olarak farklılaşır. Yine bu eşitliğe dayalı olarak güvenirlik gerçek puan varyansının gözlenen puan varyansına oranı olarak ifade edilebilir. Bu çerçevede iki paralel form arasındaki korelasyondan başlayarak güvenirlik kavramının gerçek puan varyansının gözlenen puan varyansına oranı olarak ifade edilişini aşağıda sunulan matematiksel terimlerle açıklayabiliriz.
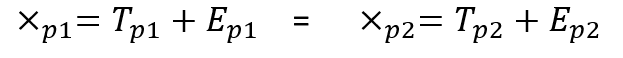
Yukarıda birinci ve ikinci paralel formlar için belirtilen iki eşitlikten de ortalama puanları çıkartarak fark puanlarını elde edebiliriz.
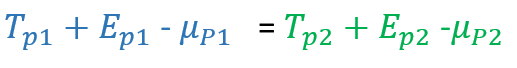
Gösterim kolaylığı sağlaması açısından fark puanlarını küçük harflerle ifade edelim.
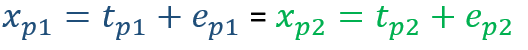
Kovaryansın ve onun standart hale dönüştürülmüş formu olan korelasyonun (sürekli veriler için) formülünü dikkate aldığımızda;
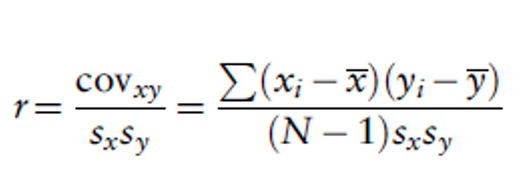
İki paralel form arasındaki korelasyonu aşağıdaki gibi ifade edebiliriz.
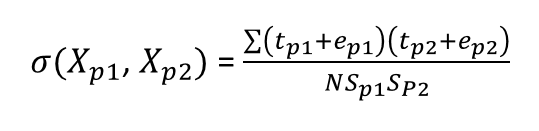
Formülün pay kısmında basit bir içler dışlar çarpımı yapıp payda kısımlarını da ayırınca sırasıyla aşağıdaki ifadeler elde edilir.
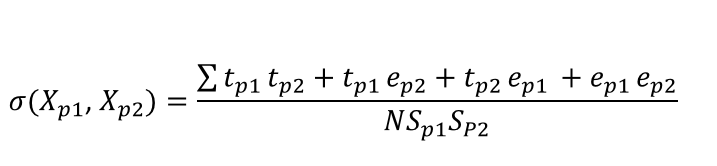
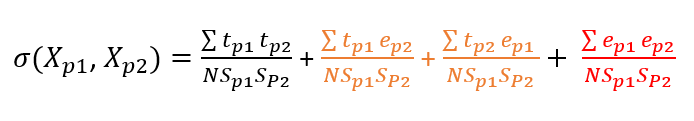
Daha önce vurgulanan klasik test kuramının üç varsayımı dikkate alındığında gerçek puan ve hata puanı arasında korelasyon olmayacağı için (2 numaralı varsayım) turuncu renk ile işaretlenen kısımlar, hata puanları arasında korelasyon olmayacağı için de (3 numaralı varsayım) kırmızı renk ile işaretlenen kısım sıfıra eşit olur ve denklemden çıkarılır.
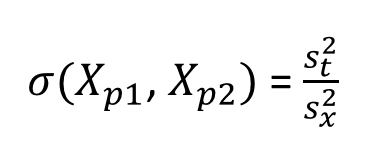
Geri kalan terimleri sadeleştirdiğimizde iki paralel form arasındaki korelasyon, diğer bir ifade ile Klasik Test Kuramına dayalı olarak güvenirlik, gerçek puan varyansının gözlenen puan varyansına oranı olarak ifade edilir.
Seçkisiz hatalar her ölçme işleminde yer alabilecek, ne yönde ve ne miktarda olduğu bilinmeyen hatalardır. Bu hata kaynakları a) ölçmenin yapıldığı bireylerden, b) ölçme işlemini yapan kişilerden, c) ölçme işleminin yapıldığı ortamdan ve d) ölçme araçlarından kaynaklanabilir. KTK’da güvenirlik belirleme yöntemleri ana hatları ile tek uygulamaya dayalı ve birden çok uygulamaya dayalı yöntemler olarak sınıflanabilir (Algina & Crocker, 1986). Açık uçlu yanıtların veya performansların değerlendirilmesinde punlayıcılar arası güvenirlik de ayrı bir yöntem olarak düşünülebilir. Erkuş vd. (2020) bunlara ek olarak maddelerin gerçek ve hata puanlarına ilişkin farklı ön kabullere dayanılarak türetilen alfa değerlerini farklı bir yöntem olarak ele almıştır. Bu elektronik kitap teorik kısımdan ziyade uygulama süreçlerine odaklandığı için bazı kısımlar göz ardı edilmiştir. Ancak okuyucuların bahsi geçen bu kaynakları incelemeleri önerilir.