3.2 İkili Puanlanan Maddeler için MTK Modelleri

Bu kısımda 1, 2 ve 3 parametreli lojistik modellere ana hatları ile değinilmiştir. Adlarından da anlaşılacağı gibi bu modelleri birbirlerinden ayıran özellik sahip oldukları parametre sayılarıdır.

3.2.1 1 Parametreli Lojistik Model

1 Parametreli lojistik modelde sadece madde güçlük parametresi (b) farklı maddeler için değişik değerler alırken ayırt edicilik parametresi (a) sabit tutulur. Şans parametresi ise (c) modele dahil edilmez, başka bir ifade ile “0”’a sabitlenir (Baker, 2016). 1 PL modelde tüm maddeler için sabit olmakla beraber bu parametre eğer “1” değerine sabitlenirse (bu durum ayırt edicilik parametresini fonksiyon içerisinde etkisiz hale getirecektir) model Rasch Modeli olarak adlandırılır. Rasch ve 1PL modeller matematiksel olarak birbirine çok benzer olmakla beraber, kuramsal açıdan bazı temel farklılıklar içerir. Aşağıda 1PL lojistik modele ilişkin olasılık fonksiyonu sunulmuştur.

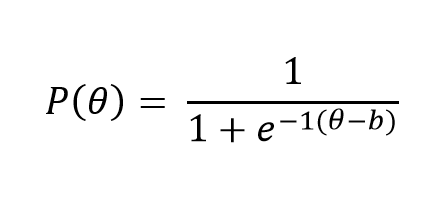
Yukarıdaki olasılık fonksiyonunda “b” madde güçlük parametresini “θ” yetenek düzeyini ifade eder. “e” ise 2.718 (exp(1)) olarak alınan matematiksel bir sabittir ve üssel fonksiyondur (Demars, 2916). “P(θ)” ise belirli bir yetenek düzeyindeki birinin belirli bir soruyu doğru yanıtlama olasılığıdır.

Aşağıda 1PL modele göre güçlük düzeyi “1.2” olan bir maddeye yetenek düzeyleri -3 ve +3 arasında değişen 61 bireyin doğru yanıt verme olasılıkları hesaplanmıştır.

teta <- seq(-3, 3, 0.1)

b<- 1.2
a<-1

P1 <- 1 / (1 + exp(-1 * (teta - b)))

print(P1)

##  [1] 0.01477403 0.01630250 0.01798621 0.01984031 0.02188127 0.02412702
##  [7] 0.02659699 0.02931223 0.03229546 0.03557119 0.03916572 0.04310725
## [13] 0.04742587 0.05215356 0.05732418 0.06297336 0.06913842 0.07585818
## [19] 0.08317270 0.09112296 0.09975049 0.10909682 0.11920292 0.13010847
## [25] 0.14185106 0.15446527 0.16798161 0.18242552 0.19781611 0.21416502
## [31] 0.23147522 0.24973989 0.26894142 0.28905050 0.31002552 0.33181223
## [37] 0.35434369 0.37754067 0.40131234 0.42555748 0.45016600 0.47502081
## [43] 0.50000000 0.52497919 0.54983400 0.57444252 0.59868766 0.62245933
## [49] 0.64565631 0.66818777 0.68997448 0.71094950 0.73105858 0.75026011
## [55] 0.76852478 0.78583498 0.80218389 0.81757448 0.83201839 0.84553473
## [61] 0.85814894

Aşağıdaki kod ile de ilgili madde için 1 PL modele dayalı madde karakteristik eğrisi oluşturulabilir.

plot(teta, P1, type="l", xlim=c(-3,3), col=2,ylim=c(0,1), lwd=3,
     main = "1 PL MODEL İÇİN MADDE KARAKTERİSTİK EĞRİSİ",
     xlab=expression(paste("yetenek, ",theta)),
     ylab=expression(paste(
       "doğru yanıt olasılığı, P(",theta,")")))

abline(v=1.2, h=0.50, lty=2,lwd=1)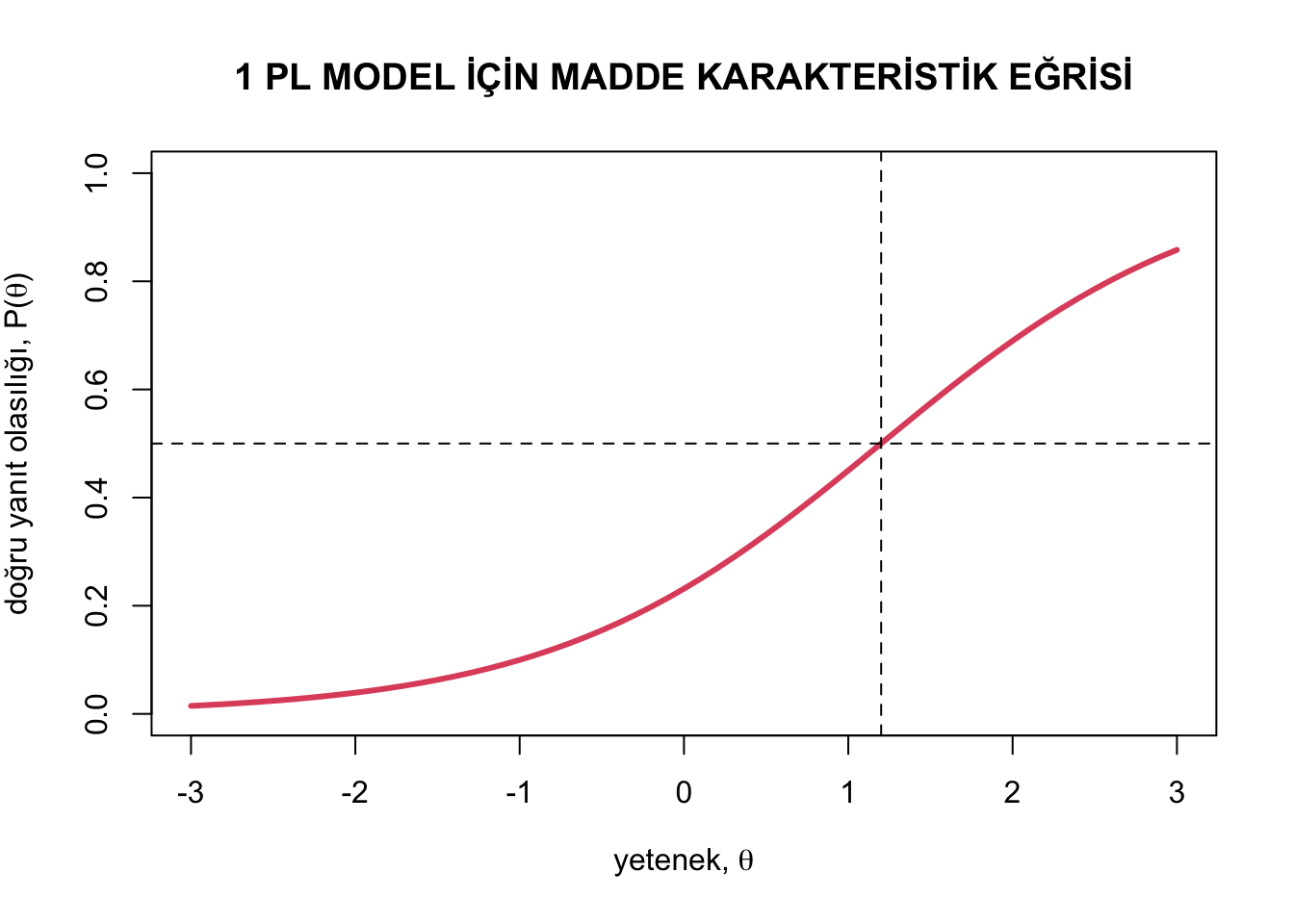

Görüldüğü gibi 1.2 yetenek düzeyinde olan bir bireyin güçlük düzeyi 1.2 olan bir maddeyi doğru yanıtlama olasılığı 0.50’dir. Bu durum ilgili yetenek düzeyi için varyansı artırır ve ileride değineceğimiz madde bilgi fonksiyonunu maksimize eder. Doğru yanıtlanma olasılığı, yetenek düzeyi maddenin güçlük düzeyinin üzerine çıktıkça aratacak, madde güçlük düzeyinin altına indikçe azalacaktır. Bu durum madde güçlük ve yetenek parametresinin aynı ölçek düzeyinde gösterilebilmesinin bir sonucudur ve MTK’nın KTK’ya göre güçlü bir yanıdır.

Aşağıdaki kodlarda “mkegraf” isimli basit bir fonksiyon tanımlanmıştır. Akabinde bu fonksiyon kullanılarak madde ayırt edicilikleri 1’e sabitlenmiş ancak madde güçlük düzeyleri sırsıyla, 0, 1 ve 1.5 olan üç maddeye ilişkin madde karakteristik eğrileri sunulmuştur.

mkegraf <- function(b, a, c=0, renk=NULL) {
  par(lab=c(7,3,3))
  teta <- seq(-3, 3, .1)
  P <- c + (1 - c)* ( 1 / (1 + exp(-a * (teta - b) ) ) )
  plot(teta, P, type="l", col=renk,lwd=2, xlim=c(-3,3), ylim=c(0,1),
       xlab="Yetenek", ylab="Doğru yanıt olasılığı")
}

mkegraf(b=0,a=1,renk="red")  # madde 1

par(new=TRUE)

mkegraf(b=1,a=1,renk="blue")  # madde 2

par(new=TRUE)

mkegraf(b=1.5,a=1,renk="orange") # madde 3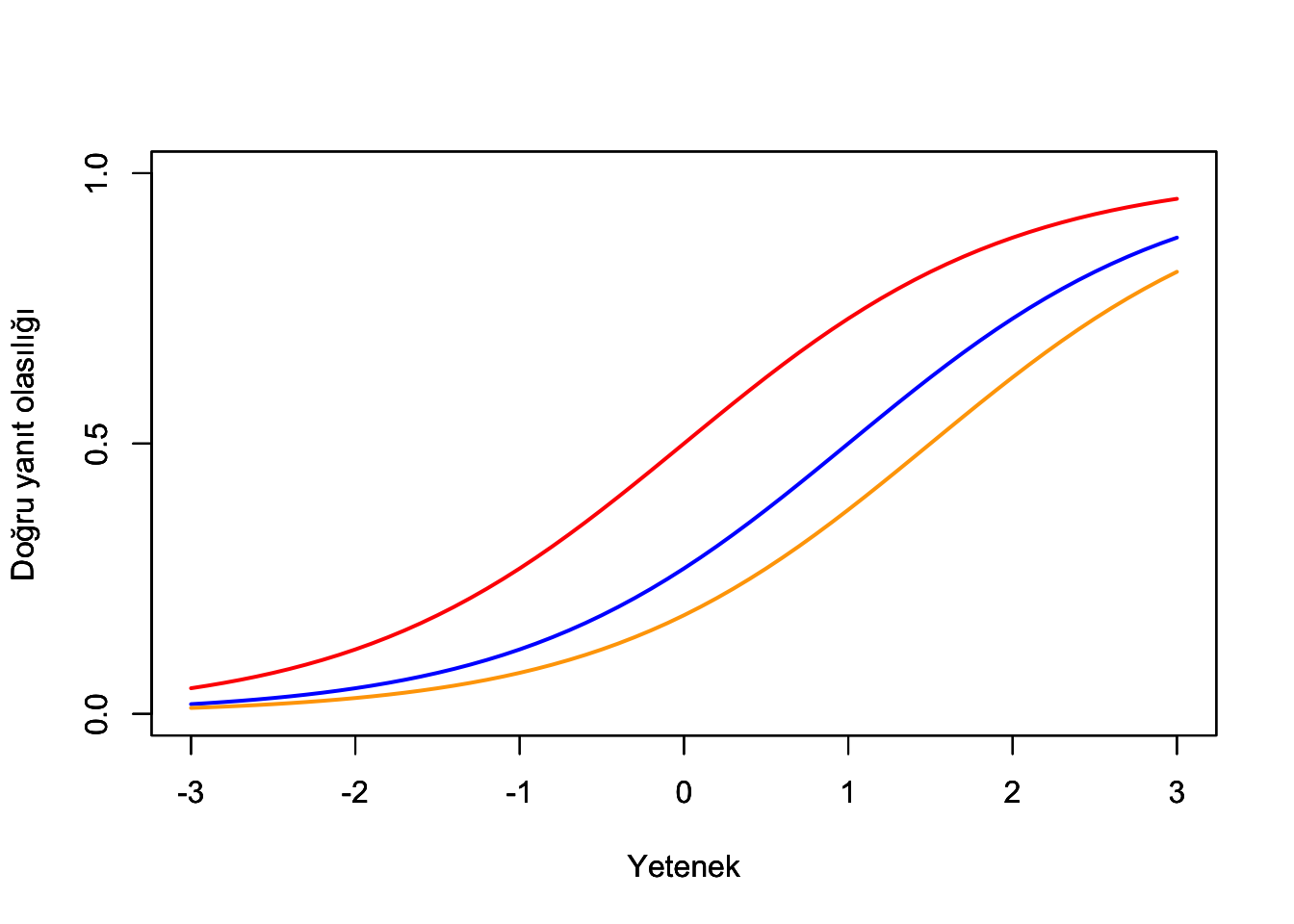

Görüldüğü gibi her üç maddenin de a parametresi aynı olduğu için eğriler birbirleri ile çakışmamaktadır.

---

3.2.2 2 Parametreli Lojistik Model

2 parametreli lojistik modelde ise 1PL modelden farklı olarak madde güçlüğü parametresinin (b) yanı sıra madde ayırt edicilik parametresi (a) de farklı maddeler için değişik değerler alır. Başka bir ifade ile “P(θ)” kestiriminde “a” parametresi de dikkate alınır ancak şans parametresi (c) yine “0” değerinde sabit tutulur.

Aşağıda 2 PL modele ilişkin olasılık fonksiyonu sunulmuştur.

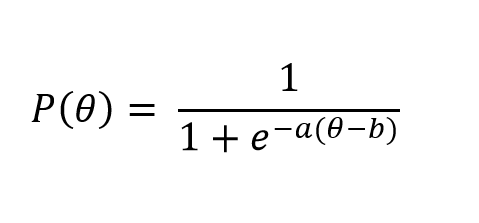
2PL model için yukarıda verilen olasılık fonksiyonundaki tek fark “a” parametresinin fonksiyona dahil edilmesidir.

Aşağıda 2PL modele göre güçlük düzeyi “0.65” madde ayırt edicilik düzeyi ise “1.4” olan bir maddeye yetenek düzeyleri -3 ve +3 arasında değişen 61 bireyin doğru yanıt verme olasılıkları hesaplanmıştır.

teta <- seq(-3, 3, 0.1)
b<- 0.65
a <- 1.4

P2 <- 1 / (1 + exp(-a * (teta - b)))

print(P2)

##  [1] 0.005999867 0.006895273 0.007923242 0.009103059 0.010456706 0.012009204
##  [7] 0.013788989 0.015828314 0.018163691 0.020836345 0.023892689 0.027384811
## [13] 0.031370932 0.035915846 0.041091278 0.046976146 0.053656652 0.061226163
## [19] 0.069784783 0.079438549 0.090298145 0.102477033 0.116088922 0.131244469
## [25] 0.148047198 0.166588614 0.186942614 0.209159365 0.233258936 0.259225101
## [31] 0.286999837 0.316479106 0.347510538 0.379893568 0.413382421 0.447692090
## [37] 0.482507142 0.517492858 0.552307910 0.586617579 0.620106432 0.652489462
## [43] 0.683520894 0.713000163 0.740774899 0.766741064 0.790840635 0.813057386
## [49] 0.833411386 0.851952802 0.868755531 0.883911078 0.897522967 0.909701855
## [55] 0.920561451 0.930215217 0.938773837 0.946343348 0.953023854 0.958908722
## [61] 0.964084154

Aşağıdaki kod ile de ilgili madde için 2 PL modele dayalı madde karakteristik eğrisi oluşturulabilir.

plot(teta, P2, type="l", xlim=c(-3,3), col=2,ylim=c(0,1), lwd=3,
     main = "2 PL MODEL İÇİN MADDE KARAKTERİSTİK EĞRİSİ",
     xlab=expression(paste("yetenek, ",theta)),
     ylab=expression(paste(
       "doğru yanıt olasılığı, P(",theta,")")))
abline(v=0.65, h=0.50, lty=2,lwd=1)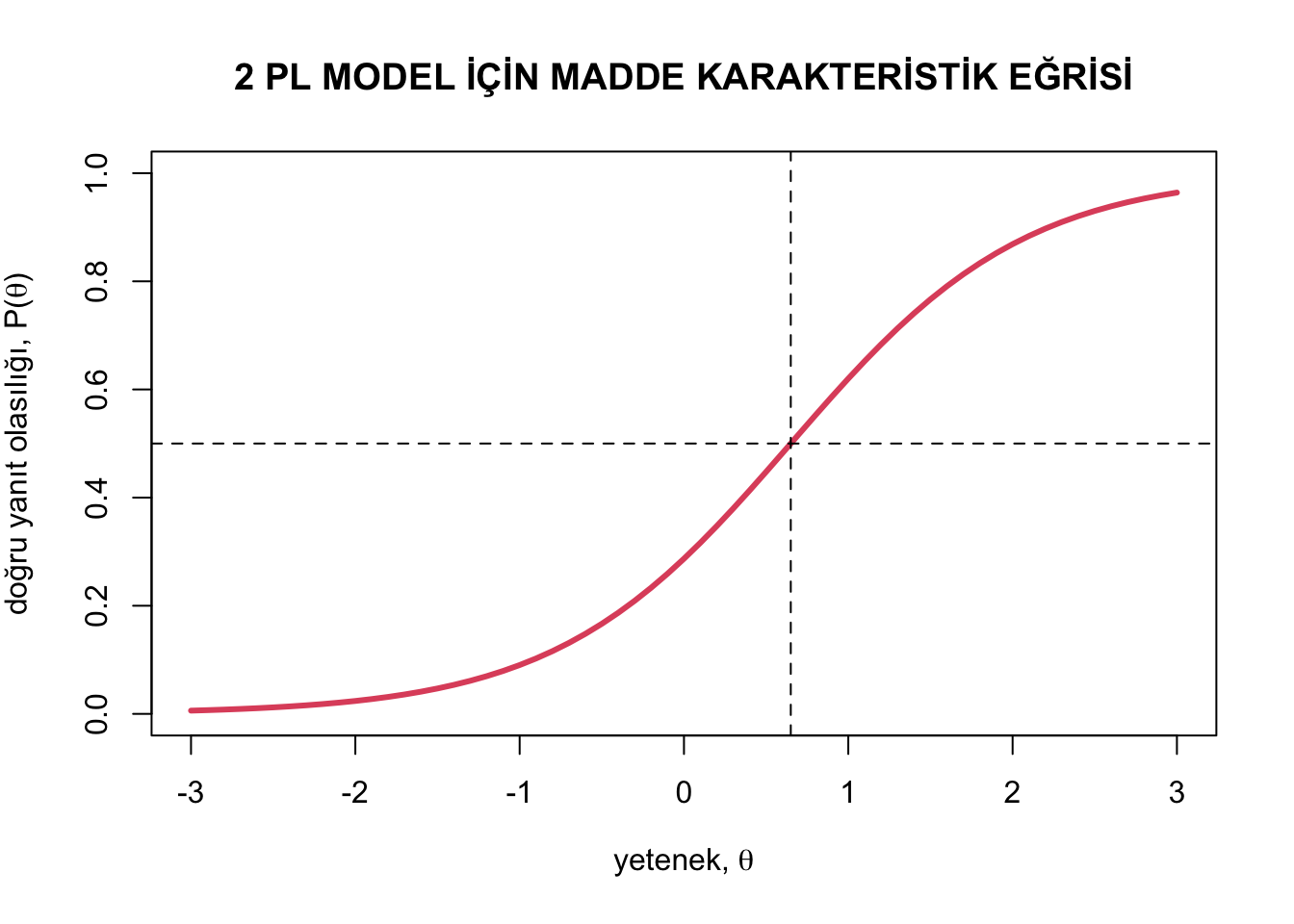

Aşağıda az önce oluşturduğumuz “mkfgraf” isimli fonksiyondan faydalanılarak 2 PL modele göre hem güçlük hem ayırt edicilik parametreleri farklı olan 3 maddeye ilişkin Madde karakteristik eğrileri oluşturulmuştur.

mkegraf(b=-0.90,a=0.50,renk="red") # madde 1

par(new=TRUE)

mkegraf(b=0.80,a=1,renk="blue") # madde 2

par(new=TRUE)

mkegraf(b=1.2,a=1.5,renk="orange") # madde 3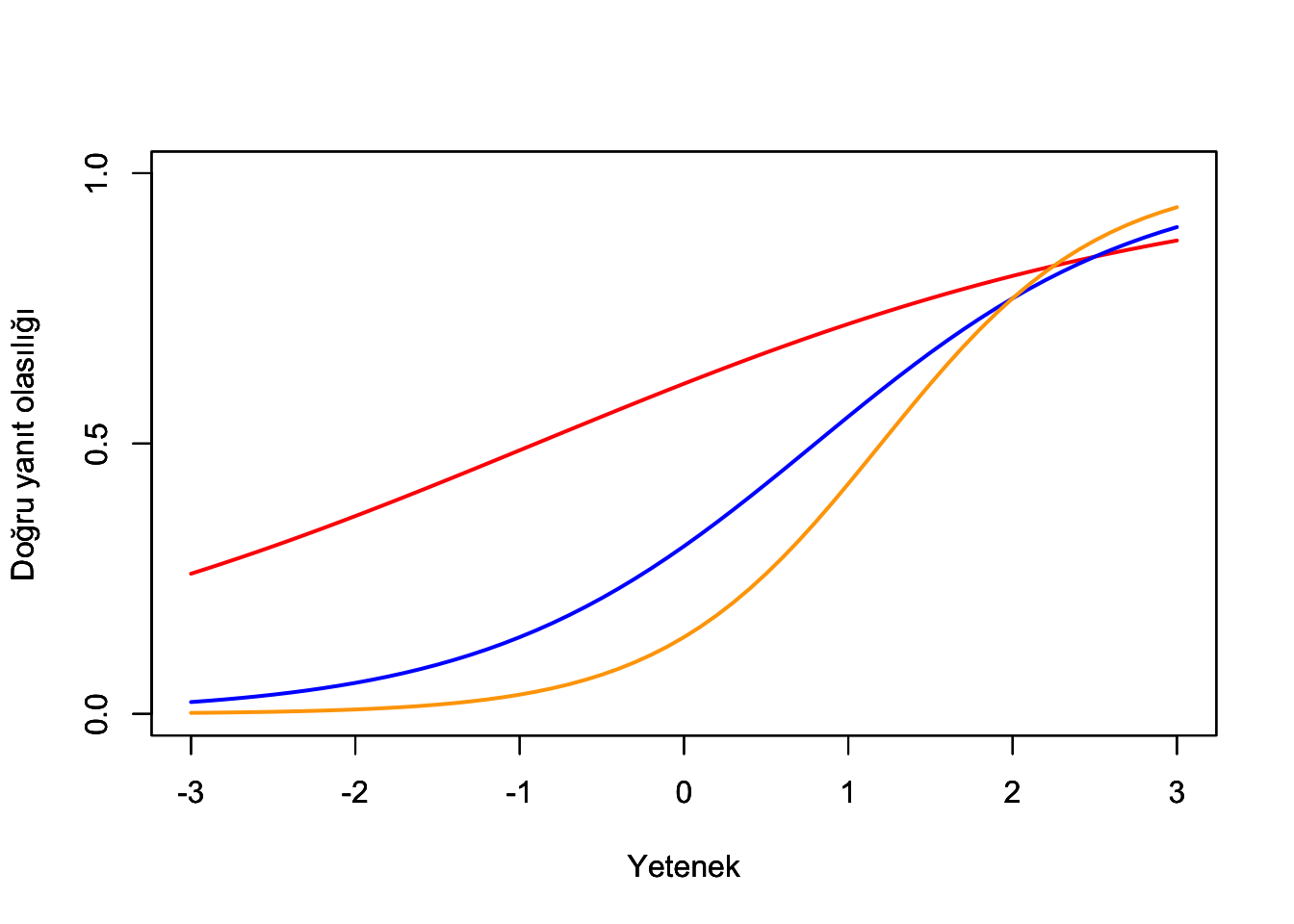

Grafikte görüldüğü gibi 1PL modelden farklı olarak 2 PL modelde a parametreleri farklılaştığı için madde karakteristik eğrilerinin çakışması söz konusudur.

---

3.2.3 3 Parametreli Lojistik Model

3 parametreli lojistik model ise 2PL’den farklı olarak şans parametresini de üçüncü bir parametre olarak olasılık fonksiyonuna ekler (Baker & Kim 2017). Özellikle şansla doğru yanıtı bulma olasılığının olduğu çoktan seçmeli sınav türlerinin kullanıldığı durumlarda 3PL model kullanılabilir. 3PL modele ilişkin olasılık fonksiyonu aşağıdaki gibidir.

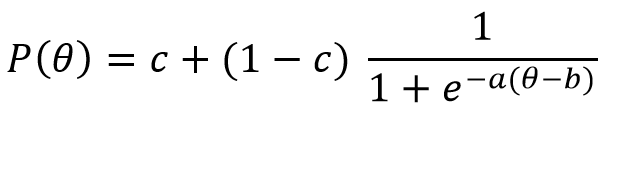
3PL modelde 2 PL modelden farklı olarak şans parametresi (c), başka bir ifade ile şansla maddeyi doğru yanıtlama olasılığı fonksiyona dahil edilmiştir. Şans parametresi teorik olarak 0 ve 1 arasında değişebilmekle beraber 0.35 üzerindeki değerler pratik nedenlerden dolayı genel olarak kabul edilmez. Baker ve Kim (2017) olasılık fonksiyonuna şans parametresinin dahil edilmesi ile güçlük parametresinin tanımında değişiklik olduğunu belirtmiştir. 1PL ve 2PL modelde hatırlayacağınız gibi b parametresi maddeyi doğru yanıtlama olasılığının 0.50 olduğu yetenek düzeyidir. Ancak işin içine şans parametresi (c) girince madde karakteristik eğrisinin en düşük değeri sıfır değil c parametresi olarak kabul edilir. Bu sebeple madde güçlük parametresinin yetenek ölçeği üzerindeki yeri değişebilir.

Aşağıda 3PL modele göre güçlük düzeyi “0.65” madde ayırt edicilik düzeyi ise “1.4” ve şans parametresi “0.25” olan bir maddeye, yetenek düzeyleri -3 ve +3 arasında değişen 61 bireyin doğru yanıt verme olasılıkları hesaplanmıştır.

teta <- seq(-3, 3, 0.1)
b<- 0.65
a <- 1.4
c<-0.25

P3<-c + (1 - c)* ( 1 / (1 + exp(-a * (teta - b) ) ) )

print(P3)

##  [1] 0.2544999 0.2551715 0.2559424 0.2568273 0.2578425 0.2590069 0.2603417
##  [8] 0.2618712 0.2636228 0.2656273 0.2679195 0.2705386 0.2735282 0.2769369
## [15] 0.2808185 0.2852321 0.2902425 0.2959196 0.3023386 0.3095789 0.3177236
## [22] 0.3268578 0.3370667 0.3484334 0.3610354 0.3749415 0.3902070 0.4068695
## [29] 0.4249442 0.4444188 0.4652499 0.4873593 0.5106329 0.5349202 0.5600368
## [36] 0.5857691 0.6118804 0.6381196 0.6642309 0.6899632 0.7150798 0.7393671
## [43] 0.7626407 0.7847501 0.8055812 0.8250558 0.8431305 0.8597930 0.8750585
## [50] 0.8889646 0.9015666 0.9129333 0.9231422 0.9322764 0.9404211 0.9476614
## [57] 0.9540804 0.9597575 0.9647679 0.9691815 0.9730631

plot(teta, P3, type="l", xlim=c(-3,3), col=2,ylim=c(0,1), lwd=3,
     main = "3 PL MODEL İÇİN MADDE KARAKTERİSTİK EĞRİSİ",
     xlab=expression(paste("yetenek, ",theta)),
     ylab=expression(paste(
       "doğru yanıt olasılığı, P(",theta,")")))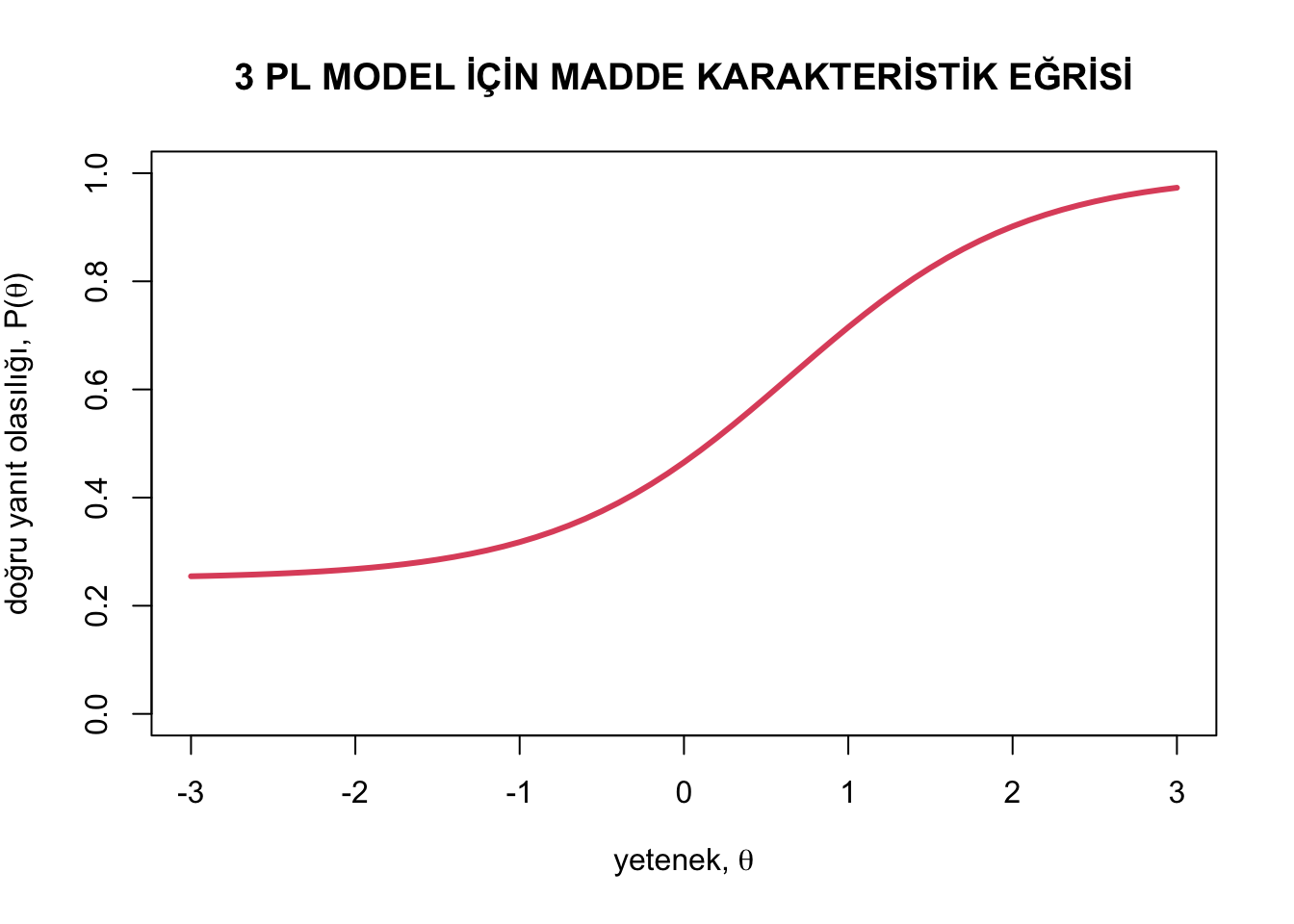

Yukarıdaki grafiğe dikkat ederseniz madde karakteristik eğrisinin başlangıç düzeyi “0” değil c parametresinin değeri olan 0.25’tir.

Aşağıda az önce oluşturduğumuz “mkfgraf” isimli fonksiyondan faydalanılarak 3 PL modele göre hem güçlük hem ayırt edicilik hem de şans parametreleri parametreleri farklı olan 3 maddeye ilişkin madde karakteristik eğrileri oluşturulmuştur.

mkegraf(b=-0.90,a=0.50, c=0.10,renk="red") # madde 1

par(new=TRUE)

mkegraf(b=0.80,a=1, c=0.20, renk="blue")  # madde 2

par(new=TRUE)

mkegraf(b=1.2,a=1.5,c=0.30,renk="orange") # madde 3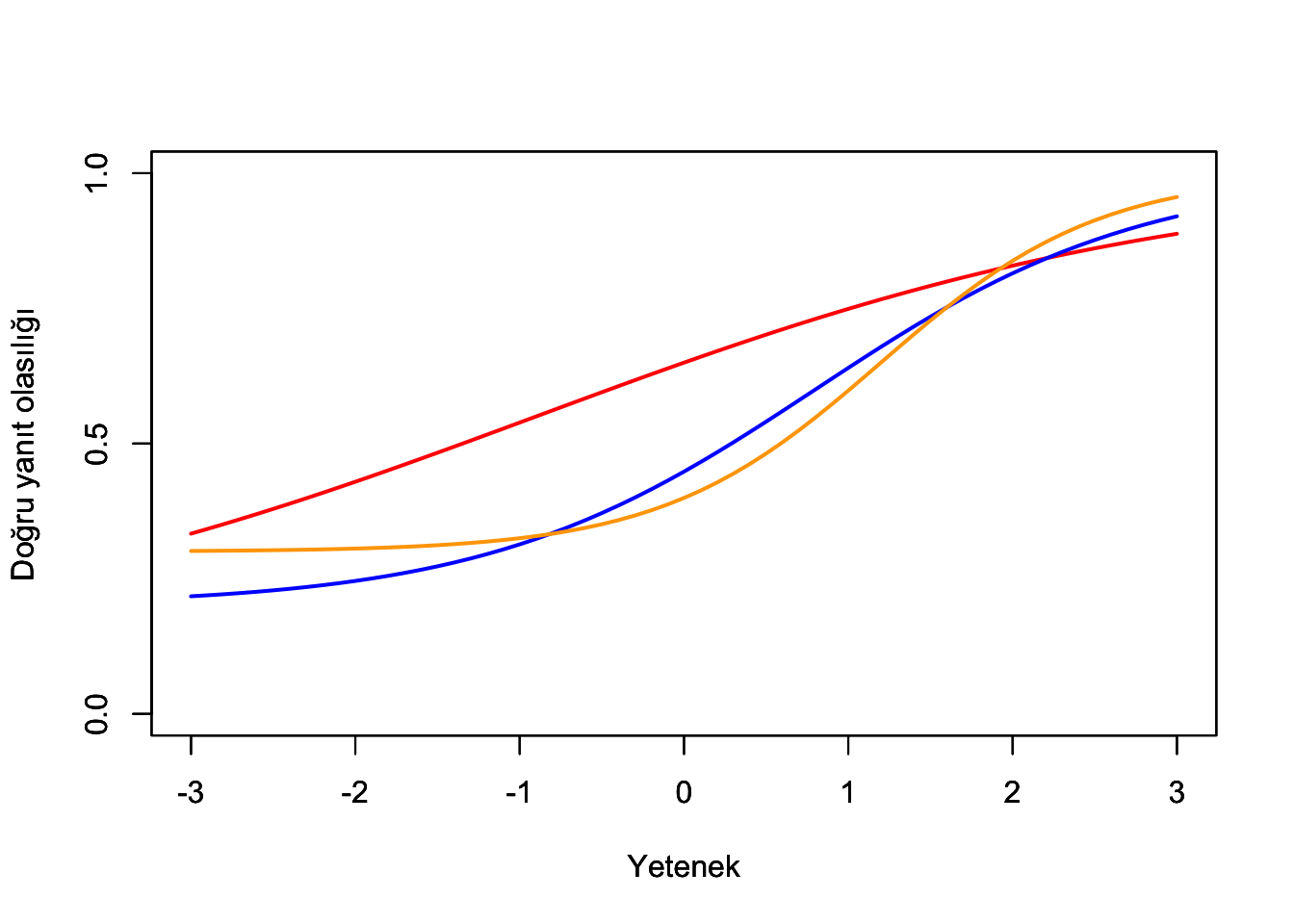

Yukarıdaki grafikte görüldüğü gibi 3 PL modelde 3 maddeye ilişkin madde karakteristik eğrilerinin başlangıç noktaları 1PL ve 2PL modelden farklı olarak değişmektedir.

---

3.2.4 Madde Bilgi Fonksiyonu ve Test Bilgi Fonksiyonu

Madde tepki kuramında bir maddeye ilişkin bilgi miktarı farklı yetenek düzeylerinde hesaplanabilir. Doğal olarak tek bir madde üzerinden hesaplandığında elde edilecek bilgi miktarı düşük olacaktır (Baker& Kim, 2017). Ancak bir maddenin hangi yetenek düzeyindeki bireyler için yüksek bilgi verdiğinin bilinmesi önemlidir. Doğal olarak bir madde varyansının en yüksek olduğu, başka bir ifade ile madde güçlük düzeyinin 0.50 olduğu durumda madde bilgi fonksiyonu en yüksek seviyesini alır. 1PL modele ilişkin madde bilgi fonksiyonu aşağıdaki gibi tanılanır.

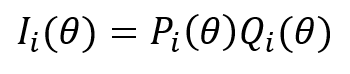
Aşağıdaki kodlarda 1PL modele göre madde güçlüğü 1.2 ve ayırt ediciliği 1 olan bir madde için madde bilgi fonksiyonunun hesaplanma ve grafiğinin çizilme sürecindeki işlemler özetlenmiştir.

teta<-seq(-6,6,0.1)
b<-1.2
a<-1

P <- 1 / (1 + exp(-1 * (teta - b))) # 1PL modele göre doğru yanıtlanma olasılığının hesaplanması

Q<-1-P                           # Yanlış yanıtlanma olasılığının hesaplanması
I<-P*Q                           # Madde bilgi fonksiyonunun hesaplanması

plot(teta,I, type="l",col="red",lwd=2,# Madde bilgi fonksiyonu grafiğinin çizilmesi
main="Madde Bilgi Fonksiyonu", xlab="Yetenek", ylab="Bilgi")
abline(v=1.2, lty=2,lwd=1)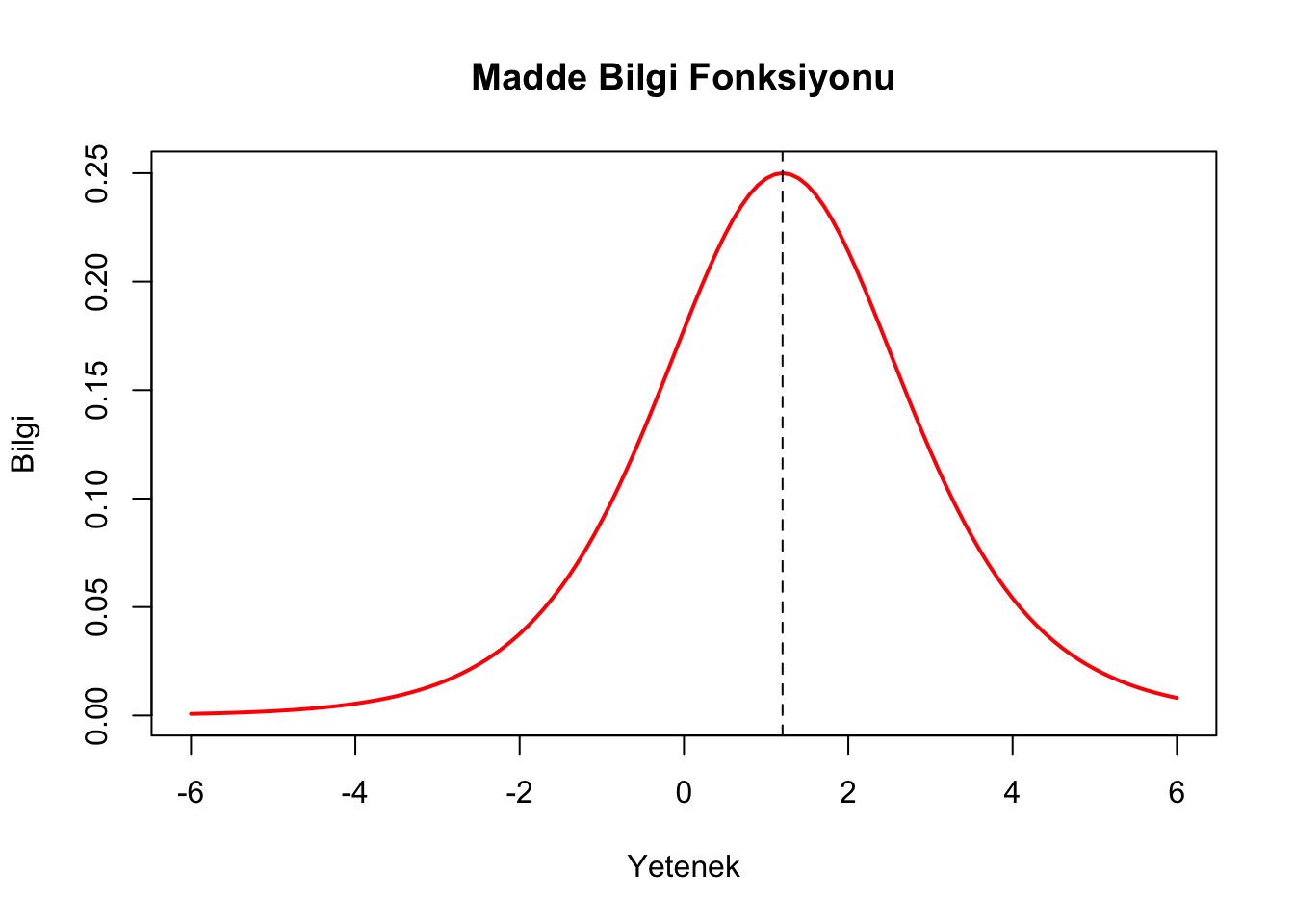

Madde bilgi fonksiyonunda görüldüğü gibi madde en yüksek bilgiyi madde güçlük düzeyi olan 1.2 yetenek düzeyinde sağlamaktadır. Kabaca maddenin -1 ile 3 arasındaki yetenek düzeyleri için nispeten daha uygun olduğu ifade edilebilir. Yetenek düzeyi -4 ve aşağısında olan ve 6 ve yukarısında olan bireyler için ise madde bilgi fonksiyonu çok düşüktür ve bu madde belirtilen yetenek düzeylerindeki bireyler için uygun değildir.

2 PL ve 3PL modeller için madde bilgi fonksiyonu sırasıyla aşağıdaki gibi ifade edilir.

2PL için madde bilgi fonksiyonu:

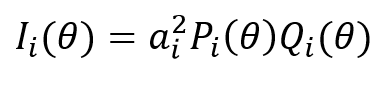
3PL için madde bilgi fonksiyonu:

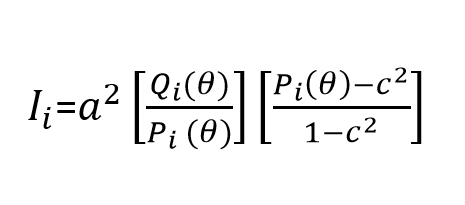
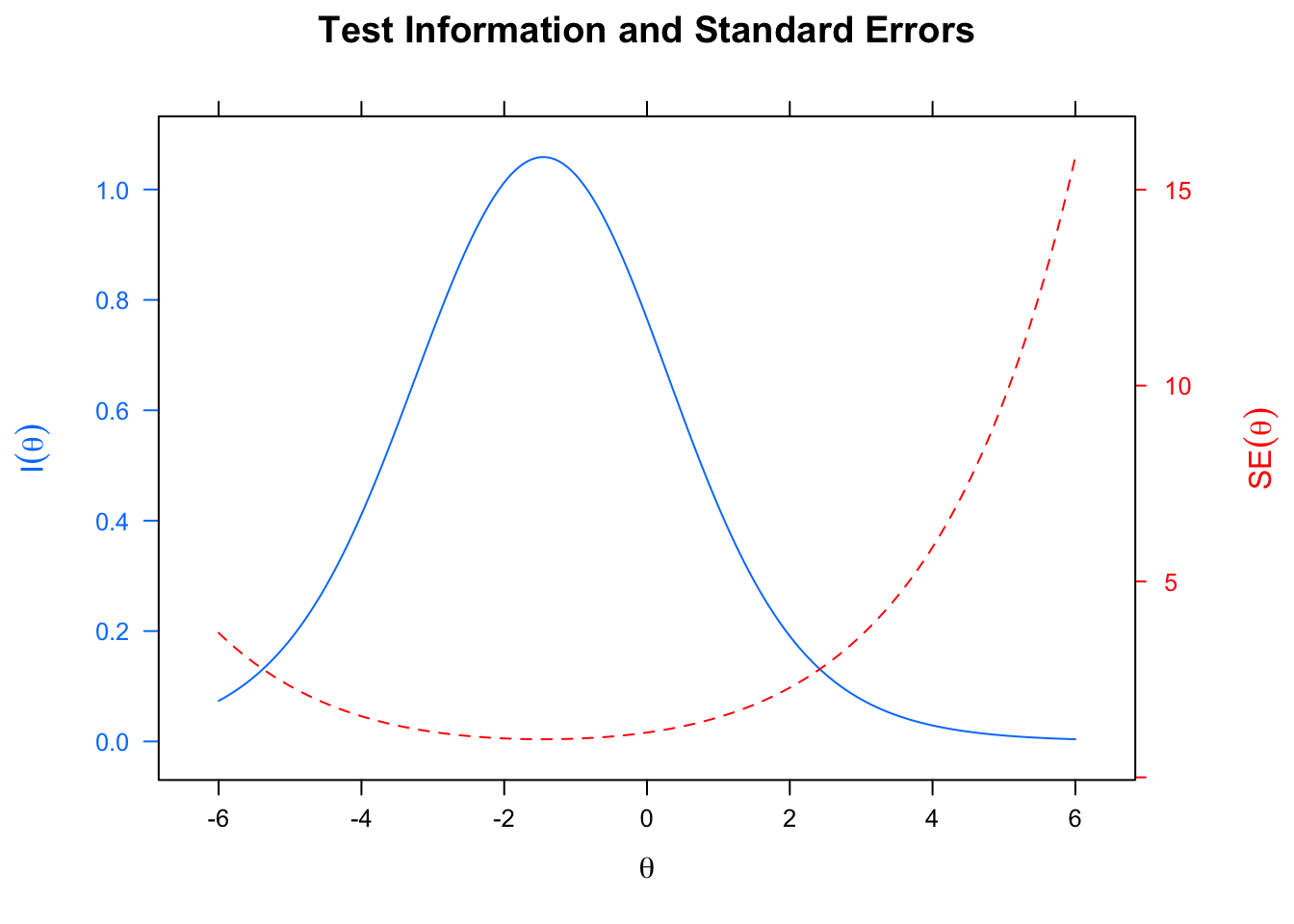
Test bilgi fonksiyonu ise belirli bir yetenek düzeyindeki madde bilgi fonksiyonlarının toplamına eşittir. Doğal olarak test bilgi fonksiyonu tek bir maddenin bilgi fonksiyonundan yüksek olacaktır. Yine test bilgi fonksiyonunun tanımından dolayı uzun testler kısa testlere kıyasla yeteneğe ilişkin daha duyarlı ölçümler yapabilir (Baker & Kim 2017). Test bilgi fonksiyonu standart hata ile negatif bir korelasyon gösterir. Yani test bilgi fonksiyonunun en yüksek olduğu yetenek düzeylerinde standart hata en düşük değeri alacaktır. Aşağıda standart hata değerlerini de içeren örnek bir test bilgi fonksiyonu grafiği sunulmuştur.