2.2 Birden Çok Uygulamaya Dayalı Güvenirlik Belirleme Yöntemleri

Eşdeğer Formlar Yöntemi Eşdeğer formlar ya da bir diğer adıyla paralel form yönteminde iki eşdeğer form aynı gruba aynı koşullar altında uygulanır ve aralarındaki ilişki düzeyi incelenir. Ancak bu yöntemin bazı pratik sınırlılıkları mevcuttur. İlk olarak hangi paralel formun önce uygulandığı sonuçta farklılıklara yol açabilir. Bazı zayıf öğrenciler birinci uygulama sonucunda deneyim elde edeceklerinden ikinci uygulamada daha yüksek bir performans sergileyebilirler. Ya da tam tersi olarak birinci uygulamada yorulan bazı öğrencilerin performansı ikinci uygulamada düşebilir. Diğer bir sınırlılık ise iki formun eşdeğer ya da paralel olarak kabul edilebilmesi için koşulların yerine getirilmesinin zorluğudur.

Test Tekrar Test Yöntemi aynı testin aynı bireylere aynı koşullar altında fakat farklı zamanlarda uygulanmasını içerir. Akabinde iki uygulama arasındaki korelasyon incelenir. Bu yöntemde iki ölçüm arası geçen zaman önem teşkil eder. Ölçülecek yapının özelliğine bağlı olarak bu sürenin belirlenmesi gerekir. Eğer ölçülen psikolojik yapı “tutum” gibi kısa sürede değişmesi zor olan bir özellik ise bu süre daha uzun tutulabilir veya “başarı” gibi dış etmenlere bağlı olarak değişimi daha kolay olan bir özellikse daha kısa tutulabilir. Ancak yaygın olarak birinci ve ikinci ölçüm arasında 2 hafta gibi bir süre olması uygun kabul edilir.

Test-tekrar test güvenirlik katsayısı ölçme aracı ile ölçülen özelliğin zaman içerisinde farklılaşmadığının göstergesidir. Başka bir ifade ile ölçme aracının zamana karşı değişmezliğinin bir göstergesidir. Test-tekrar test güvenirlik katsayısının hesaplanma sürecinde yaygın olarak iki farklı zaman diliminde (Z1, Z2) ölçüm gerçekleştirilir.

Test-tekrar test güvenirlik katsayısının hesaplanmasında yaygın olarak iki ölçüm arasındaki ilişkinin gücü dikkate alınır. İki ölçüm arasında yüksek pozitif bir korelasyon (r>0.80) elde edilmesi istenen bir durumdur. Ancak şunu vurgulamak gerekir ki iki ölçüm arasındaki ilişkinin yönü ve gücü test-tekrar test güvenirlik katsayısı hakkında karar vermek için yeterli değildir. Bunun yanı sıra asıl önemli olan iki farklı zamanda elde edilen ölçümler arasındaki uyumun yüksek olmasıdır. Aynı örneklem üzerinde aynı özelliği iki defa ölçtüğümüzde, iki ölçüm arasında belirli bir düzeyde korelasyon olması zaten beklenen bir durumdur ancak iki farklı ölçme neticesinde elde edilen puanlar arasındaki uyum düşük olabilir. (Bland & Altman, 1986).

Bu nedenle iki ölçüm arasındaki ilişkinin yanı sıra tutarlılığı veya uyum düzeyini belirlemek için sınıfiçi korelasyon katsayının (ICC - Intra-Class Correlation Coefficient) kullanılması uygun olacaktır (Weir ,2005). Aslında puanlayıcılar arası güvenirlik hesaplamalarında kullanılan ICC test-tekrar test güvenirlik katsayısının hesaplanmasında da kullanılan bir yöntemdir. ICC “tek yönlü rastgele model”, “iki yönlü rastgele model” ve ” iki yönlü karışık etki modeli” olmak üzere 3 farklı model içerir. Ayrıca mutlak uyum (absolute agreement) ve tutarlılık (consistencey) olmak üzere iki farklı boyut içermektedir. Tutarlılık iki ölçüm arasındaki ilişkinin gücü ve yönüne odaklanırken mutlak uyum iki ölçüm arasındaki puanların değişmezliğine odaklanır. Bu anlamda test-tekrar test güvenirlik katsayının hesaplanmasında mutlak uyum yönteminin kullanılması daha sağlıklı sonuçlar üretecektir.

ICC hesaplamasına geçmeden önce karşılaştırma yapmak için test-tekrar test güvenirlik katsayını iki ölçüm arasındaki korelasyon katsayısını (Pearson korelasyon katsayısı) hesaplayarak belirleyelim. Bunun için öncelikli olarak arasında ilişki olan iki veri seti oluşturalım. Bunun için “rnorm” fonksiyonundan faydalanalım.

set.seed(1234)  # her seferinde seçkisiz veri üretiminde aynı değerlere ulaşma için sabitleme işlemi

# ortalaması 60 standart sapması 10 olan normal dağılımdan gelen 50 veri üretimi

t1<- round(rnorm(50,60,10)) 

# ilk veri seti ile ilişkili olan veri üretlelim 

t2<- round(t1+10+rnorm(50,0,2))

print(t1) ; print(t2)

##  [1] 48 63 71 37 64 65 54 55 54 51 55 50 52 61 70 59 55 51 52 84 61 55 56 65 53
## [26] 46 66 50 60 51 71 55 53 55 44 48 38 47 57 55 74 49 51 57 50 50 49 47 55 55

##  [1] 54 72 79 45 74 76 67 63 67 59 66 65 62 70 80 73 63 64 65 95 71 64 65 76 67
## [26] 56 73 59 71 60 81 65 60 65 56 59 49 56 67 63 84 60 64 69 59 61 57 59 67 69

Şimdi “cor” fonksiyonu ile bu iki ölçüm arasındaki ilişki düzeyini hesaplayalım ve “plot” fonksiyonu ile saçılma grafiğini çizelim.

cor(t1,t2)

## [1] 0.9733784

plot(t1,t2,col=2, main = "Birinci ve İkinci Ölçüme ilişkin Saçılma Grafiği",xlab="Birinci Ölçüm", ylab="İkinci Ölçüm")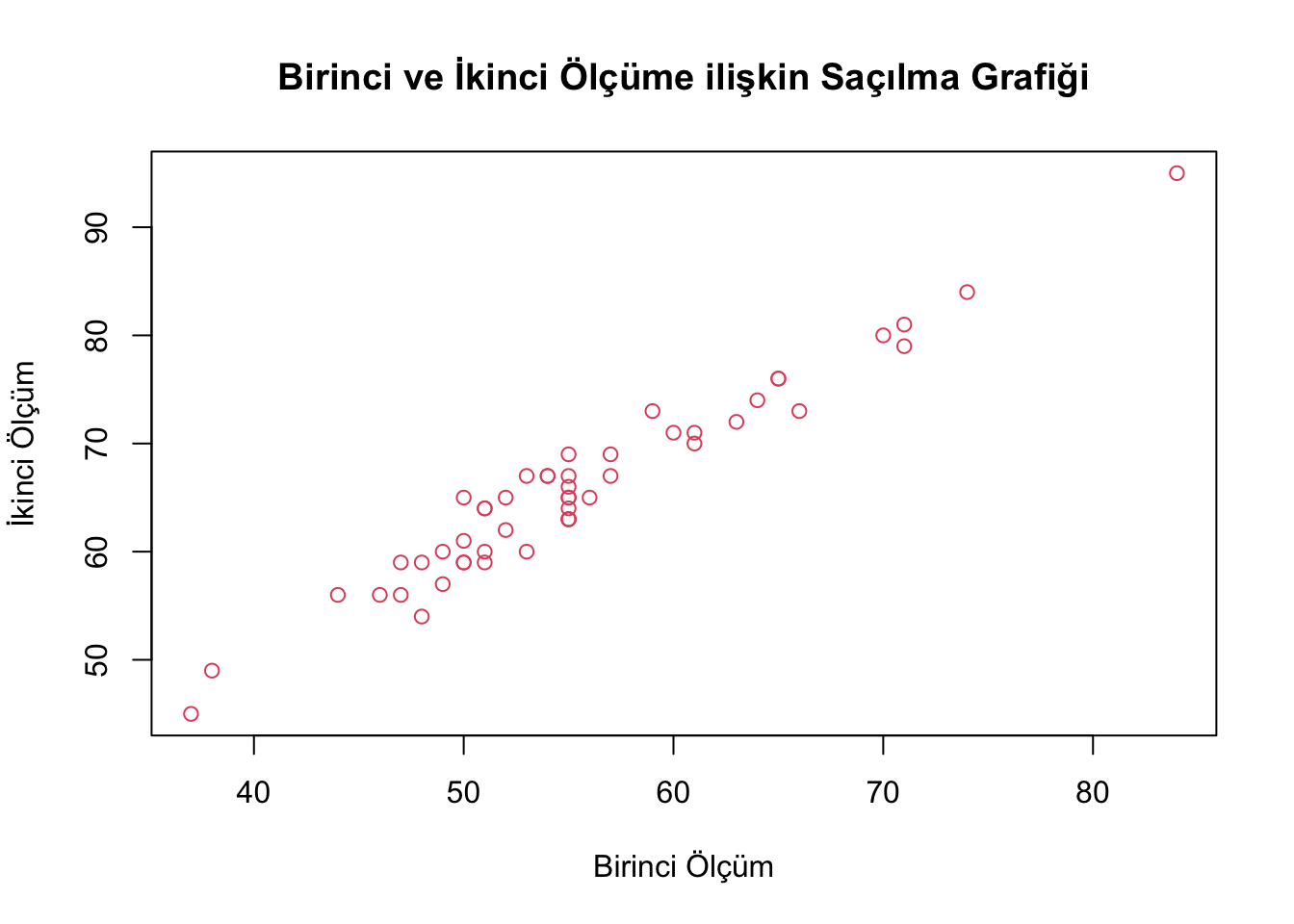

Görüldüğü gibi iki ölçüm arasında pozitif, yüksek bir ilişki (0.98) mevcuttur. Acaba bu bulgular ışığında test-tekrar test güvenirlik katsayısının uygun olduğu veya ölçme sonuçlarına zamandan kaynaklı bir hata bulaşmadığını iddia edebilir miyiz? Şimdi aynı veri seti üzerinde sınıf-içi korelasyon katsayısını (ICC) hesaplayarak sonuçları karşılaştıralım.

R’da test-tekrar test güvenirlik katsayının hesaplanması sürecinde “irr” paketinden faydalanılabilir (Gamer, Lemon & Singh, 2019). Öncelikli olarak bu paketin indirilmesi ve sonrasında “library” komutu ile çağrılması gerekmektedir.

install.packages("irr")

library(irr)

ICC hesaplanmasında “irr” paketinde bulunan “icc” fonksiyonundan faydalanırız. Bu fonksiyonun ilk argümanı her sütununda aynı bireylere ilişkin farklı ölçümleri içeren matris ya da veri çerçevesi (data frame)dir. Puanlayıcılar arası güvenirliğin hesaplandığı durumlarda sütunlarda farklı puanlayıcılar yer alırken test-tekrar test güvenirliğinin hesaplanması sürecinde farklı zamanlarda yapılan ölçüm sonuçları yer alır. Bu nedenle daha önce oluşturduğumuz, birinci ve ikinci ölçümleri ifade eden vektörleri “cbind” fonksiyonu ile birleştirip matris formatına dönüştürelim.

t12<-cbind(t1,t2) # matris oluşturma

colnames(t12)<- c("Ölçüm 1","Ölçüm 2") # sütun isimleri verme

head(t12)# ilk altı satırı sunma

##      Ölçüm 1 Ölçüm 2
## [1,]      48      54
## [2,]      63      72
## [3,]      71      79
## [4,]      37      45
## [5,]      64      74
## [6,]      65      76

“irr” fonksiyonun ikinci argümanı “model”dir. Burada daha önce bahsettiğimiz 3 modelden birisi (“tek yönlü rastgele model”, “iki yönlü rastgele model” ve ” iki yönlü karışık etki modeli”) seçilir. Tek yönlü rastgele model puanlayıcılar arası güvenirlik hesaplandığı durumlarda her bireyin puanlayıcı evreninden rastgele seçilen puanlayıcı tarafından puanlandığı durumlarda kullanılır. Burada puanlayıcılar rastgele etki olarak ele alınır. Pratikte bu durumun sağlanması pek mümkün değildir. Özellikle test-tekrar test güvenirlik katsayısının hesaplanması sürecinde uygun bir model olmayacaktır. iki yönlü rastgele modelde ise bireyler ve puanlayıcılar rastgele etki modeli olarak görülür. İki yönlü karışık etki modelinde ise puanlayıcılar sabittir ve puanlayıcılar sabit etkiye sahiptir ve elde edilen sonuçlar diğer puanlayıcılara genellenemez. Ancak test tekrar test güvenirlik katsayısının hesaplanmasında en uygun model budur (Koo & Li 2016). Bu nedenle argümanımodel="twoway" şeklinde kullanacağız. Diğer argüman olan “type” ile iki ölçüm arasındaki ilişki düzeyine mi yoksa mutlak uyumamı bakılacağı belirlenir. Burada test tekrar test güvenirlik katsayısı içintype="agreement" şeklinde kullanılması gerekmektedir. Bir diğer önemli argüman ise unit argümanıdır. Bu argüman unit="single" olarak kullanıldığı zaman iki ölçüm arasındaki uyum her birey bazında karşılaştırılır. Argüman unit="average" şeklinde kullanıldığı zaman ise birinci ve ikinci ölçümlerin ortalamaları bağlamında bir uyum değeri elde edilir. Test-tekrar test güvenirlik katsayısı için ölçüm ortalamaları bağlamında bir uyum değeri hesaplanabilmekle beraber bir ölçme aracının zamana yönelik değişmezliğinin doğru belirlenebilmesi için birey karşılaştırmaları bazında da uyum değerlerinin hesaplanması önemli bir kanıt olacaktır. icc fonksiyonu ön tanımlı olarak belirlenen başka argümanlara da sahiptir. Detaylı bilgi için ?icc komutunu çalıştırabilirsiniz.”

icc(t12,"twoway","agreement", unit="single")

##  Single Score Intraclass Correlation
## 
##    Model: twoway 
##    Type : agreement 
## 
##    Subjects = 50 
##      Raters = 2 
##    ICC(A,1) = 0.581
## 
##  F-Test, H0: r0 = 0 ; H1: r0 > 0 
##  F(49,1.11) = 73.8 , p = 0.0741 
## 
##  95%-Confidence Interval for ICC Population Values:
##   -0.017 < ICC < 0.878

icc(t12,"twoway","agreement", unit = "average")

##  Average Score Intraclass Correlation
## 
##    Model: twoway 
##    Type : agreement 
## 
##    Subjects = 50 
##      Raters = 2 
##    ICC(A,2) = 0.735
## 
##  F-Test, H0: r0 = 0 ; H1: r0 > 0 
##  F(49,1.09) = 73.8 , p = 0.0763 
## 
##  95%-Confidence Interval for ICC Population Values:
##   -0.034 < ICC < 0.935

Elde edilen çıktı incelendiğinde test-tekrar test güvenirlik katsayısının birey bazlı karşılaştırmada 0.581, ortalama bazlı karşılaştırmada ise 0.735 olduğu görülmektedir. Her iki değerde Pearson korelasyon katsayısı ile elde ettiğimiz sonuca (0.97) kıyasla çok daha düşüktür.

Aşağıda test tekrar test güvenirlik katsayısının hesaplanması sürecinde sınıfiçi korelasyon katsayısının kullanımını içeren bir shiny uygulaması bulunmaktadır. Bu uygulama iki yönlü modelde, birim olarak iki ölçümün ortalamasını dikkate alan ve iki ölçüm arasındaki uyuma odaklı bir sınıfiçi korelasyon katsayısı hesaplamaktadır.

Bu uygulamayı kullanmak için

“veri yükleme” kısmına tıklayın. Veri setinizin “sav” uzantılı (SPSS) bir dosya olması gerekmektedir. Veriniz eğer hatasız yüklenmiş ise ekranda size bildirilecektir. Verinin yükleme süreci yaklaşık 5-30 sn arasında değişkenlik göstermektedir. Eğer “sav” uzantılı olmayan bir veri seti yüklenirse sistem hata verecektir.
Akabinde veri setinizde yer alan değişkenlerin isimleri “Birinci ölçüm için Değişken Seçiniz” ve “İkinci ölçüm için Değişken Seçiniz” başlıklı kısımlarda gözükecektir.
Sonuç olarak üretilen çizelgede “ICC” başlığı altında sınıfiçi korelasyon katsayısı ve her iki ölçümü ortak olarak yanıtlayan kişi sayısı yer almaktadır. Shiny uygulamasının bulunduğu pencerenin sağ tarafında bulunan çubuğu aşağı çekerek analiz sonuçlarını görebilirsiniz.