6.2 Farklı Modellere Göre İkili puanlanan (1-0) Veri Seti Üretimi
Bu bölümde sırası ile Rasch, 1PL, 2PL ve 3PL modeller için ikili puanlanan (1-0) veri üretimi örneklendirilmiştir. Bu modellere ilişkin detaylar 3. Bölümde açıklandığı için burada sunulmamıştır. Bilgi eksiği olan okuyucuların 3. Bölüme göz atmaları önerilir.
6.2.1 Rasch Modeline Dayalı Veri Üretimi
Bu kısımda Rasch modeli ile uyumlu (model veri uyumu sağlanmış) ikili puanlanan verilerin üretilme süreci R programlama dili aracılığı ile açıklanmıştır. Rasch modelinin matematiksel gösterimi aşağıda verilmiştir.
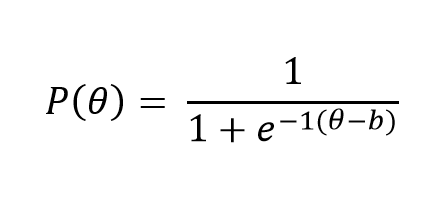
Rasch modeli çerçevesinde hatırlayacağınız gibi “a” (ayırt edicilik) parametresi “1” değerine sabitlenmekteydi. Veri üretimi sürecinde ilk olarak üretilecek veri seti için madde sayısının, maddelerin güçlük düzeylerinin, yanıtlayıcı sayısının ve yanıtlayıcıların yetenek düzeylerinin belirlenmesi gerekmektedir.
n<-200 # Yanıtlayıcı sayısı
madde<- 15 # madde sayısı
a<-rep(1,madde) # madde sayısı kadar a parametresi (1'e sabitlenmiş)
b<- runif( madde, -2, 2) # -2 +2 aralığında üretilen b parametreleri
teta<-rnorm(n,0,1)Yukarıdaki kodlarda görüldüğü gibi sırası ile yanıtlayıcı ve madde sayıları akabinde ise “a” ve “b” parametreleri üretilmiştir. Rasch modelinde “a” parametresi “1”’e sabitlendiği için “rep” fonksiyonu ile madde sayısı kadar “1” değeri üretilmiştir. Güçlük parametresi ise “runif” fonksiyonuyla üretilmiştir. “runif” tek biçimli dağılıma uygun olarak rastgele veri üretmede kullanılan bir fonksiyondur. Ancak benzer amaçla farklı dağılımlara yönelik rastgele veri üretme fonksiyonları da kullanılabilir (“rnorm”,“rlnorm” vb). Yetenek düzeyleri ise “rnorm” fonksiyonu ile yanıtlayıcı sayısı kadar üretilmiştir.
Şimdi sırada yanıtlayıcıların yetenek düzeylerinin elde edilmesi gerekmektedir. Ancak öncesinde hesaplama kolaylığı sağlamak amacıyla satırlarda yanıtlayıcılar sütunlarda ise maddelerin bulunduğu bir matris oluşturalım.
Bu matriste her bir satırlarda her bir madde için üretilen “b” parametreleri bulunmaktadır.
## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] -1.9290786 -1.9290786 -1.9290786 -1.9290786 -1.9290786 -1.9290786
## [2,] 0.9496943 0.9496943 0.9496943 0.9496943 0.9496943 0.9496943
## [3,] -1.5874052 -1.5874052 -1.5874052 -1.5874052 -1.5874052 -1.5874052
## [4,] -0.9485516 -0.9485516 -0.9485516 -0.9485516 -0.9485516 -0.9485516
## [5,] 0.8608104 0.8608104 0.8608104 0.8608104 0.8608104 0.8608104
## [6,] -1.8336350 -1.8336350 -1.8336350 -1.8336350 -1.8336350 -1.8336350
## [7,] 0.9943333 0.9943333 0.9943333 0.9943333 0.9943333 0.9943333
## [8,] 2.4461111 2.4461111 2.4461111 2.4461111 2.4461111 2.4461111
## [9,] -0.1847496 -0.1847496 -0.1847496 -0.1847496 -0.1847496 -0.1847496
## [10,] 0.6387348 0.6387348 0.6387348 0.6387348 0.6387348 0.6387348Yukarıdaki kodlarda görüldüğü gibi oluşturulan matriste satır ve sütunlarda madde sayısı ( veya üretilen “b” parametresi kadar) kadar tekrar ettirilen yetenek parametreleri yer almaktadır. Gösterim kolaylığı açısından ilk 10 satır ve ilk 6 madde burada sunulmuştur. Dikkat edeceğiniz gibi her yanıtlayıcı (satır) için tüm maddelere aynı değerler atanmıştır. Her bir satır için farklı sütunlarda yer alan değerler ilgili yanıtlayıcının yetenek düzeyidir.
Madde parametreleri bilindiği için yukarıda sunulmuş olan lojistik model yardımıyla yanıtlayıcı yetenek düzeyleri (teta) kestirilebilir.
yetenekm1<- t (apply( yetenekm , 1, '-', b) )
yetenekm2 <- t( apply( yetenekm1, 1,'*',a) )
ols<- 1 / ( 1 + exp(-yetenekm2) )
pteta <- matrix( ols, ncol = madde)
pteta[1:10,1:6]## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 0.07828427 0.1855289 0.02585713 0.02570310 0.1487131 0.1967554
## [2,] 0.60177893 0.8020958 0.32077799 0.31944328 0.7565841 0.8133726
## [3,] 0.10676527 0.2427512 0.03600951 0.03579724 0.1973314 0.2563504
## [4,] 0.18461872 0.3778224 0.06608493 0.06570745 0.3177343 0.3950410
## [5,] 0.58029850 0.7876070 0.30172801 0.30043751 0.7398441 0.7995030
## [6,] 0.08545424 0.2003859 0.02837316 0.02820459 0.1612053 0.2122770
## [7,] 0.61242611 0.8090862 0.33058070 0.32922497 0.7647106 0.8200541
## [8,] 0.87094044 0.9476415 0.67835406 0.67701451 0.9327963 0.9511302
## [9,] 0.32704931 0.5658652 0.13185651 0.13115609 0.4998996 0.5836149
## [10,] 0.52545879 0.7480964 0.25708817 0.25591861 0.6948903 0.7615353Yukarıdaki kodlarda Rasch Modeline dayalı olarak yetenek kestirimleri gerçekleştirilmiştir. Öncelikli olarak “yetenekm” isimli matriste yer alan üretilen yetenek değerlerinden “b” parametreleri çıkarılmıştır. Bunun için “apply” fonksiyonundan faydalanılmıştır. Bu işlem “for” döngüleri ile de gerçekleştirilebilir ancak biz burada pratik olması amacı ile “apply” fonksiyonundan faydalandık apply( yetenekm , 1, '-', b). Daha sonra bu yeni oluşan matrisi “t” fonksiyonu ile tranpoze ettik (satır ve sütunların yerini değiştirdik) ve “yetenekm1” isimli bir obje içerisine kaydettik yetenekm1<- t (apply( yetenekm , 1, '-', b) ). Akabinde matristeki yeni değeler “a” paramatresi ile çarpılarak benzer bir işlem tekrar edilmiş ve “yetenekm2” isimli bir obje içerisine kaydedilmiştir yetenekm2 <- t( apply( yetenekm1, 1,'*',a) ). Daha sonra en son oluşturulan “yetenekm2” isimli matris üzerinden yetenek parametresi (teta) kestirilmiştir ve “ols” isimli bir obje içerisinde aktarılmıştır. ols<- 1 / ( 1 + exp(-yetenekm2) ). Son olarak elde edilen değerler “pteta” isimli bir objeye kaydedilmiştir. Pratiklik açısından burada matrisin ilk 10 satırı ve ilk 6 sütunu sunulmuştur.
Şimdiki aşamada ise belirtilen özelliklere uygun 1-0 matrisi oluşturulacaktır. Bunun için “sapply” fonksiyonu içerisinde “rbinom” fonksiyonundan faydalandık.
İlk başta biraz karışık gibi gözüken yukarıdaki kodları açıklamada fayda vardır. Öncelikli olarak “rbinom” fonksiyonu burada önemli bir işleve sahiptir. Hatırlayacağınız gibi “rbinom” fonksiyonu binom dağılımına uygun rastgele veri üretmede kullanılan bir fonksiyondu. Örneğin rbinom( n=1, size=1, prob=0.50) kodu %50 olasılıkla bir tane “0” veya “1” değeri üretir. Eğer “prob” argümanını “1” değerine yaklaştırırsak rastgele üretilecek değerin “1” olma olasılığı artar. Benzer şekilde “0” değerine yaklaşırsa da üretilen değerin “0” olma olasılığı artacaktır.
Burada “rbinom” fonksiyonu içerisindeki “prob” argümanında az önce her madde için ürettiğimiz yanıtlama olasılıklarını kullanırsak matristeki her gözenek için “1” veya “0” değerlerini elde edebiliriz. Örneğin 1. kişi ve 1. madde için rbinom(n=1,s,ze=1,prob=0.7672704) komutu ile bir değer üretebiliriz. 1. kişinin 1. maddeyi doğru yanıtlama olasılığı yüksek olduğu için bu işlemin sonucu büyük (%77) olasılıkla “1” olacaktır.
Tabiki de madde sayısı x birey sayısı kadar gözeneğimiz olduğu için bu işlemi tüm gözenekler için tekrar ettirmemiz gerekmektedir. Bunun için “for” döngüsünden faydalanmak mümkündür. Ancak pratiklik açısından biz “sapply” fonksiyonundan faydalandık sapply ( pteta, rbinom, n = 1, size = 1 ). Daha sonra üretilen “1” ve “0” değerlerini matris yapısına dönüştürüp “yanitmat” isimli obje içerisine kaydettik yanitmat <- matrix(sapply ( pteta, rbinom, n = 1, size = 1 ) , ncol = length(b) ).
Şimdi ürettiğimiz “1-0” matrisini biraz düzenleyelim.
yanitmat2<-rbind(b,a,yanitmat)
sira<-paste0("birey",1:n)
row.names(yanitmat2)<- c("b","a",sira)
colnames(yanitmat2)<-paste0("madde",1:madde)
res<-as.data.frame(yanitmat2)
res[1:12,1:6]## madde1 madde2 madde3 madde4 madde5 madde6
## b 0.5368115 -0.4497505 1.699893 1.706026 -0.184348 -0.5223805
## a 1.0000000 1.0000000 1.000000 1.000000 1.000000 1.0000000
## birey1 0.0000000 0.0000000 0.000000 0.000000 0.000000 0.0000000
## birey2 0.0000000 0.0000000 1.000000 0.000000 1.000000 1.0000000
## birey3 0.0000000 0.0000000 0.000000 0.000000 0.000000 0.0000000
## birey4 0.0000000 1.0000000 0.000000 0.000000 0.000000 0.0000000
## birey5 1.0000000 0.0000000 0.000000 0.000000 1.000000 1.0000000
## birey6 0.0000000 0.0000000 0.000000 0.000000 1.000000 0.0000000
## birey7 1.0000000 0.0000000 0.000000 0.000000 0.000000 1.0000000
## birey8 1.0000000 1.0000000 1.000000 0.000000 1.000000 1.0000000
## birey9 0.0000000 0.0000000 0.000000 0.000000 1.000000 0.0000000
## birey10 1.0000000 1.0000000 1.000000 0.000000 1.000000 1.0000000Yukarıdaki kodlarda öncelikli olarak madde parametreleri (b,a) matrisin başına eklenmiştir. Akabinde satır ve sütun isimleri belirlenmiş ve son olarak matris “data.frame” türüne dönüştürülmüştür. Pratiklik açısından burada ilk 10 birey ve ilk 6 madde sunulmuştur.
Tüm bu yazılan kodları bir araya getiren bir fonksiyon yazmak kullanım kolaylığı sağlayacaktır. Bu fonksiyona “pl1veri” ismini verelim.
pl1veri<-function(nitem,n,a,minb,maxb){
b<- runif( nitem, minb,maxb)
theta<-rnorm(n,0,1)
yetenekm <- matrix( rep( theta, length( b ) ), ncol = length( b) )
yetenekm1<- t (apply( yetenekm , 1, '-', b) )
yetenekm2 <- t( apply( yetenekm1, 1,'*',a) )
ols<- 1 / ( 1 + exp(-yetenekm2) )
pteta <- matrix( ols, ncol = nitem)
yanitmat <- matrix(sapply ( pteta, rbinom, n = 1, size = 1 ) , ncol = length(b) )
yanitmat2<-rbind(b,a,yanitmat)
sira<-paste0("birey",1:n)
row.names(yanitmat2)<- c("b","a",sira)
colnames(yanitmat2)<-paste0("madde",1:nitem)
res<-as.data.frame(yanitmat2)
return(res)
}Bu fonksiyon girdi olarak madde sayısı (nitem), birey sayısı(n), a parametresinin değeri (a), b parametresinin en düşük değeri (minb), b parametresinin en yüksek değeri (maxb) yer almaktadır. Şimdi bu fonksiyonu kullanarak 300 kişi ve 5 madde için üretilen bir “1-0” türünde veri üretelim.
## madde1 madde2 madde3 madde4 madde5
## b -1.195975 0.8256451 -1.73028 1.163711 -1.69785
## a 1.000000 1.0000000 1.00000 1.000000 1.00000
## birey1 1.000000 1.0000000 1.00000 1.000000 1.00000
## birey2 1.000000 0.0000000 0.00000 0.000000 1.00000
## birey3 0.000000 0.0000000 1.00000 0.000000 0.00000
## birey4 1.000000 1.0000000 1.00000 0.000000 1.00000
## birey5 1.000000 0.0000000 1.00000 0.000000 1.00000
## birey6 0.000000 0.0000000 1.00000 0.000000 1.00000
## birey7 0.000000 0.0000000 1.00000 0.000000 1.00000
## birey8 1.000000 1.0000000 0.00000 0.000000 0.00000
## birey9 1.000000 0.0000000 1.00000 1.000000 1.00000
## birey10 1.000000 0.0000000 1.00000 0.000000 0.00000Şimdi yaptığımız bu işlemleri “for” döngüsünden faydalanarak tekrarlayalım. Yani belirlediğimiz özelliklere sahip örneğin 20 “1-0” türünde veri seti üretelim.
boslist<-list()
for ( i in 1:20) {
boslist[[i]]<- pl1veri(nitem=5, n=300, a=1, minb = -2, maxb = 2)
}
verilist<-boslist
verilist[[2]][1:12,]## madde1 madde2 madde3 madde4 madde5
## b 0.6220302 -0.006448179 0.4640499 -0.6815155 1.453993
## a 1.0000000 1.000000000 1.0000000 1.0000000 1.000000
## birey1 1.0000000 0.000000000 1.0000000 1.0000000 0.000000
## birey2 0.0000000 0.000000000 1.0000000 0.0000000 0.000000
## birey3 0.0000000 0.000000000 0.0000000 0.0000000 0.000000
## birey4 1.0000000 0.000000000 0.0000000 0.0000000 1.000000
## birey5 0.0000000 1.000000000 0.0000000 1.0000000 0.000000
## birey6 0.0000000 0.000000000 0.0000000 1.0000000 0.000000
## birey7 0.0000000 0.000000000 0.0000000 1.0000000 0.000000
## birey8 0.0000000 0.000000000 0.0000000 0.0000000 0.000000
## birey9 1.0000000 0.000000000 1.0000000 1.0000000 1.000000
## birey10 0.0000000 0.000000000 0.0000000 0.0000000 1.000000Burada öncelikli olarak “boslist” isimli bir boş liste oluşturduk. Ürettiğimiz her bir veri setini bu liste içerisinde muhafaza edeceğiz. Sonrasında for döngüsü içerisinde az önce yazdığımız “pl1veri” isimli fonksiyonu kullanarak 20 adet farklı veri seti ürettik. Gerçekleştirilen bu işleme replikasyon adı verilir.
Ürettiğimiz bu veriyi oluşturduğumuz boş liste içerisinde aktardık. Pratiklik açısından boş liste içerine aktardığımız 2. veri setinin belirli bir kısmı (ilk 10 birey) çıktıda sunulmuştur.
Eğer üretilen veri setlerini “R” ortamı dışına aktarmak isterseniz “dir.create” komutundan ve “write.table” fonksiyonundan faydalanabilirsiniz.
for ( i in 1:20) {
dir.create("SIMVERI")
write.table(verilist[[i]], file=paste("SIMVERI/1PL_",i,".csv", sep=""),
sep=";", row.names = FALSE, col.names=FALSE, quote=FALSE)
}Öncelikli olarak “dir.create” komutu ile verilerin muhafaza edileceği klasörün adı belirlenir. Bu klasör belirlediğiniz çalışma dizini (working directory) içerisinde yer alacaktır. Akabinde write.table fonksiyonundan faydalanırız. Bu fonksiyon içerisinde az önce ürettiğimiz verileri içeren “verilist” isimli liste türündeki objeyi kullandık. Aşağıda dışarı aktarılan verilerin çalışma dizinindeki görünümü sunulmuştur.
6.2.2 2PL ve 3PL Modeller için Simülatif Veri Üretimi
Bir önceki bölümde 1PL ve Rasch modeline uygun “1-0” yapısına sahip verilerin üretim süreci detaylı olarak sunulmuştu. Bu kısımda ise 2PL ve 3PL için veri üretim sürecini örnekledik. Ancak farklı logistik modeller için veri üretim süreci çok benzerdir. Bu nedenle 2PL ve 3PL modellere uygun veri üretim aşamaları detaylı açıklanmamış ancak veri üretiminde kullanılabilecek fonksiyonlar sunulmuştur.
Öncelikli olarak veri üretimi 2PL model için örneklendirmiştir. Hatırlatma olması amacı ile aşağıda 2PL modelin matematiksel gösterimi sunulmuştur. Hatırlanacağı gibi 2PL modelde yetenek kestirimi sürecinde madde güçlük parametresinin (b) yanı sıra madde ayırt edicilik parametresi(a) de herhangi bir değere sabitlenmez, maddeler arasında farklılaşır.
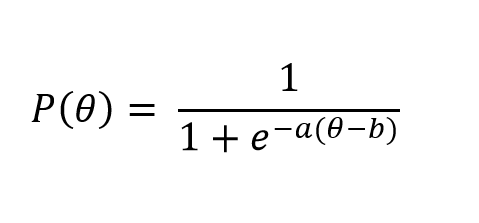
Aşağıda 2PL model için simülatif veri üretiminde kullanılabilecek bir “pl2veri” isimli fonksiyon sunulmuştur.
pl2veri<-function(nitem, n, mina, maxa, minb, maxb){
b<- runif(nitem, minb, maxb)
a<- runif(nitem, mina, maxa)
theta<-rnorm(n,0,1)
yetenekm <- matrix( rep( theta, length( b ) ), ncol = length( b) )
yetenekm1<- t (apply( yetenekm , 1, '-', b) )
yetenekm2 <- t( apply( yetenekm1, 1,'*',a) )
ols<- 1 / ( 1 + exp(-yetenekm2) )
pteta <- matrix( ols, ncol = nitem)
yanitmat <- matrix(sapply ( pteta, rbinom, n = 1, size = 1 ) , ncol = length(b) )
yanitmat2<-rbind(b,a,yanitmat)
sira<-paste0("birey",1:n)
row.names(yanitmat2)<- c("b","a",sira)
colnames(yanitmat2)<-paste0("madde",1:nitem)
res<-as.data.frame(yanitmat2)
return(res)
}“pl2veri” fonksiyonu girdi olarak madde sayısı(nitem), yanıtlayıcı sayısı (n), ayırt edicilik parametresinin en düşük ve en yüksek değerleri (mina, maxa), madde güçlüğü parametresinin en düşük ve en yüksek değerleri (minb,maxb) yer almaktadır. Bu fonksiyonun “pl1veri” isimli fonksiyondan farklı girdi olarak ayırt edicilik parametresi (a) için de en küçük en yüksek değerleri içermesidir. Şimdi bu fonksiyonu kullanarak belirtilen özelliklere sahip bir veri seti üretelim.
## madde1 madde2 madde3 madde4 madde5
## b -0.4662783 0.7303882 0.4295702 -0.4056496 -1.7219328
## a 1.0639383 0.4108444 1.8358058 1.7032356 0.6132021
## birey1 1.0000000 1.0000000 1.0000000 1.0000000 1.0000000
## birey2 1.0000000 0.0000000 0.0000000 0.0000000 1.0000000
## birey3 0.0000000 0.0000000 0.0000000 1.0000000 1.0000000
## birey4 1.0000000 0.0000000 1.0000000 1.0000000 1.0000000
## birey5 1.0000000 1.0000000 1.0000000 1.0000000 1.0000000
## birey6 1.0000000 0.0000000 0.0000000 1.0000000 0.0000000
## birey7 0.0000000 0.0000000 1.0000000 0.0000000 1.0000000
## birey8 0.0000000 1.0000000 0.0000000 1.0000000 1.0000000
## birey9 1.0000000 1.0000000 1.0000000 1.0000000 1.0000000
## birey10 0.0000000 0.0000000 1.0000000 1.0000000 1.0000000Yukarıdaki kodlarda görüldüğü gibi 500 yanıtlayıcının 5 maddeye verdikleri yanıtları içeren 2PL modele uygun bir veri seti üretilmiştir. Pratiklik açısından verinin ilk 10 yanıtlayıcıya ilişkin kısmı sunulmuştur. Veri setinin ilk iki satırında sırasıyla madde güçlük ve madde ayırt edicilik parametreleri bulunmaktadır.
Şimdi bu işlemi 20 kez tekrar ettirelim. Bu süreçte üretilen her bir veri seti bir liste içerisine aktarılmıştır. Pratik olması açısından üretilen 2. verinin ilk 10 bireyine ilişkin yanıt örüntüsü sunulmuştur.
boslist2pl<-list()
for ( i in 1:20) {
boslist2pl[[i]]<- pl2veri(nitem=5,n=500, mina=0, maxa = 2, minb=-2, maxb=2 )
}
verilist2pl<-boslist2pl
verilist2pl[[2]][1:12,]## madde1 madde2 madde3 madde4 madde5
## b 1.42747404 1.5893960 -0.22926482 0.2097319 0.85609852
## a 0.06948856 0.4459323 0.01687964 1.7483204 0.01551523
## birey1 0.00000000 0.0000000 1.00000000 0.0000000 0.00000000
## birey2 1.00000000 1.0000000 0.00000000 0.0000000 1.00000000
## birey3 0.00000000 1.0000000 1.00000000 0.0000000 1.00000000
## birey4 0.00000000 0.0000000 0.00000000 1.0000000 1.00000000
## birey5 1.00000000 0.0000000 0.00000000 1.0000000 1.00000000
## birey6 1.00000000 0.0000000 0.00000000 0.0000000 0.00000000
## birey7 0.00000000 0.0000000 1.00000000 1.0000000 1.00000000
## birey8 0.00000000 0.0000000 0.00000000 0.0000000 1.00000000
## birey9 1.00000000 0.0000000 0.00000000 1.0000000 0.00000000
## birey10 1.00000000 0.0000000 0.00000000 0.0000000 1.000000003PL model ise kitabın önceki bölümlerinde vurgulandığı gibi kestirim sürecinde madde güçlük(b) ve madde ayırt edicilik(a) parametrelerine ek olarak şans parametresini (c) de dikkate alır. 3PL modelin matematiksel kestirimi hatırlatmak amacı ile aşağıda sunulmuştur.
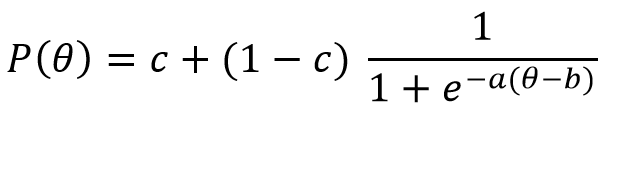
Aşağıda 3PL model için simülatif veri üretiminde kullanılabilecek “pl3veri” isimli bir fonksiyon sunulmuştur.
pl3veri<-function(nitem, n, mina, maxa, minb, maxb, minc, maxc){
b<- runif(nitem, minb, maxb)
a<- runif(nitem, mina, maxa)
c<-runif( nitem, minc, maxc)
theta<-rnorm(n,0,1)
yetenekm <- matrix( rep( theta, length( b ) ), ncol = length( b) )
yetenekm1<- t (apply( yetenekm , 1, '-', b) )
yetenekm2 <- t( apply( yetenekm1, 1,'*',a) )
ols<- 1 / ( 1 + exp(-yetenekm2) )
ols1<-t(apply(ols,1,'*',(1-c)))
ols2<-t(apply(ols1,1,'+',c))
pteta <- matrix( ols2, ncol = nitem)
yanitmat <- matrix(sapply ( pteta, rbinom, n = 1, size = 1 ) , ncol = length(b) )
yanitmat2<-rbind(b,a,c,yanitmat)
sira<-paste0("birey",1:n)
row.names(yanitmat2)<- c("b","a","c",sira)
colnames(yanitmat2)<-paste0("madde",1:nitem)
res<-as.data.frame(yanitmat2)
return(res)
}“pl3veri” fonksiyonu girdi olarak madde sayısı(nitem), yanıtlayıcı sayısı (n), ayırt edicilik parametresinin en düşük-en yüksek değerleri (mina, maxa), madde güçlüğü parametresinin en düşük - en yüksek değerleri (minb,maxb) ve şans parametresinin en yüksek - en düşük değerleri yer almaktadır. Bu fonksiyonun “pl2veri” isimli fonksiyondan farkı girdi olarak şans parametresi (c) için de en küçük en yüksek değerleri içermesidir. Şimdi bu fonksiyonu kullanarak belirtilen özelliklere sahip bir veri seti üretelim.
orn_3plveri<-pl3veri(nitem=5,n=1000, mina=0, maxa = 2, minb=-2, maxb=2, minc = 0, maxc = 0.20 )
orn_3plveri[1:13,]## madde1 madde2 madde3 madde4 madde5
## b 1.20693189 -1.65079494 1.3906334 -0.4389244 1.19521817
## a 0.08573934 0.96329956 0.8251399 1.9686939 0.03401851
## c 0.16771704 0.02569857 0.1420408 0.1121400 0.08232844
## birey1 1.00000000 1.00000000 1.0000000 1.0000000 0.00000000
## birey2 1.00000000 0.00000000 0.0000000 0.0000000 1.00000000
## birey3 0.00000000 0.00000000 0.0000000 1.0000000 1.00000000
## birey4 0.00000000 0.00000000 0.0000000 0.0000000 0.00000000
## birey5 0.00000000 1.00000000 0.0000000 1.0000000 0.00000000
## birey6 1.00000000 1.00000000 0.0000000 1.0000000 0.00000000
## birey7 0.00000000 1.00000000 1.0000000 1.0000000 1.00000000
## birey8 1.00000000 1.00000000 0.0000000 1.0000000 1.00000000
## birey9 1.00000000 1.00000000 0.0000000 1.0000000 1.00000000
## birey10 1.00000000 1.00000000 0.0000000 0.0000000 1.00000000Yukarıdaki kodlarda görüldüğü gibi 1000 yanıtlayıcının 5 maddeye verdikleri yanıtları içeren 3PL modele uygun bir veri seti üretilmiştir. Pratiklik açısından verinin ilk 10 yanıtlayıcıya ilişkin kısmı sunulmuştur. Veri setinin ilk üç satırında sırasıyla madde güçlük, madde ayırt edicilik ve şans parametreleri bulunmaktadır.
Şimdi bu işlemi 30 kez tekrar ettirelim. Bu süreçte üretilen her bir veri seti bir liste içerisine aktarılmıştır.
boslist3pl<-list()
for (i in 1:30) {
boslist3pl[[i]]<- pl3veri(nitem=5,n=1000, mina=0, maxa = 2,
minb=-2, maxb=2, minc = 0, maxc = 0.20 )
}Yukarıdaki kodlarda görüldüğü gibi önce boş bir liste oluşturulmuş ve “for” döngüsü ile 30 farklı veri seti üretilerek bu veri setleri “boslist3pl” isimli boş liste içerisine aktarılmıştır. 2PL model için verilen örnekten farklı olarak bu sefer liste içerisine kaydettiğimiz veri setlerini R ortamı dışarısına aktaralım.
for ( i in 1:30) {
dir.create("3PLVERI")
write.table(boslist3pl[[i]], file=paste("3PLVERI/3PL_",i,".csv", sep=""),
sep=";", row.names = FALSE, col.names=FALSE, quote=FALSE)
}Burada öncelikli olarak çalışma dizini içerisinde “3PLVERI” isimli bir klasör oluşturulmuştur dir.create("3PLVERI"). Sonrasında ise “write.table” fonksiyonu ile “;” ile ayrılmış “csv” uzantısına sahip şekilde veriler ” 3PLVERI” isimli klasöre aktarılmıştır.
 ********************
********************