4.4 İkili Puanlanan Maddeler İçeren bir Ölçek için AFA Hesaplama

İkili puanlanan maddeler için AFA hesaplama sürecinde (daha öncede belirtildiği gibi faktör çıkarma yöntemi olarak Temel Bileşen Analizini kullandık.) maddeler arasındaki korelasyonlar temel alınır. Biz çoğu zaman çoklu puanlanan maddelerin (Likert tipi vb) sürekli olduğu varsayımından hareketle (Bu varsayım pür istatistikçiler tarafından eleştirilebilmektedir) korelasyon matrisini oluştururken verilerin sürekli olmasını gerektiren Pearson korelasyon katsayısını (“cor” fonksiyonu ile) kullanırız. Ancak veri setimiz ikili olarak puanlanıyorsa (örneğin 1- 0 şeklinde puanlanan çoktan seçmeli test gibi) korelasyon matrisini oluştururken Pearson korelasyon katsayısını kullanmamız uygun olmaz. O nedenle iki kategorik değişken arasındaki korelasyonun hesaplanmasında kullanabileceğimiz tetrakorik korelasyon katsayısı üzerinden korelasyon matrisinin hesaplanması gerekmektedir.

Bu durumun örneklendirilmesi için “ltm” paketinde yer alan “LSAT” veri seti kullanılmıştır. “psych” paketinde yer alan “tetrachoric” fonksiyonu ile tetrakorik korelasyon matrisi oluşturulmuştur. tet.matris$rho konutu ile çıktı içerisinden korelasyon matrisi çekilmiştir.

library(ltm)
library(psych)
nrow(LSAT)

## [1] 1000

tet.matris<- tetrachoric(LSAT)

tet.matris$rho

##            Item 1    Item 2    Item 3    Item 4     Item 5
## Item 1 1.00000000 0.1703045 0.2275272 0.1071868 0.06650107
## Item 2 0.17030454 1.0000000 0.1890846 0.1111478 0.17241177
## Item 3 0.22752724 0.1890846 1.0000000 0.1866732 0.10549299
## Item 4 0.10718677 0.1111478 0.1866732 1.0000000 0.20092050
## Item 5 0.06650107 0.1724118 0.1054930 0.2009205 1.00000000

Bu aşamadan sonra yapılacak işlemler çoklu puanlanan maddelerdekine çok benzerdir. Tek farklılık kullanılan korelasyon matrisinin türüdür. Bu nedenle faktör sayısını belirleme adımını burada örneklendirip diğer adımları göz ardı edeceğiz.

model<-principal(tet.matris$rho,nfactors = 5, rotate = "none")

library(hornpa)

PA1<-hornpa(k=5,size=100,reps=500)

## 
##  Parallel Analysis Results  
##  
## Method: pca 
## Number of variables: 5 
## Sample size: 100 
## Number of correlation matrices: 500 
## Percentile: 0.95 
## 
## Compare your observed eigenvalues from your original dataset to the 95 percentile in the table below generated using random data. If your eigenvalue is greater than the percentile indicated (not the mean), you have support to retain that factor/component. 
##  
##  Component  Mean  0.95
##          1 1.285 1.425
##          2 1.118 1.201
##          3 0.991 1.059
##          4 0.872 0.952
##          5 0.734 0.833

 plot(model$values, type = "b",col=2,lty=1, main = " YAMAÇ GRAFİĞİ VE PARALEL ANALİZ", xlab = "Faktör Sayısı",
      ylab = " Öz Değer")
      lines(PA1$Mean,type="b",col=1,lty=2)
      legend("topright", legend=c("PA Ortalama", "Öz Değer"), col=1:2,lty=c(2,1), lwd=2)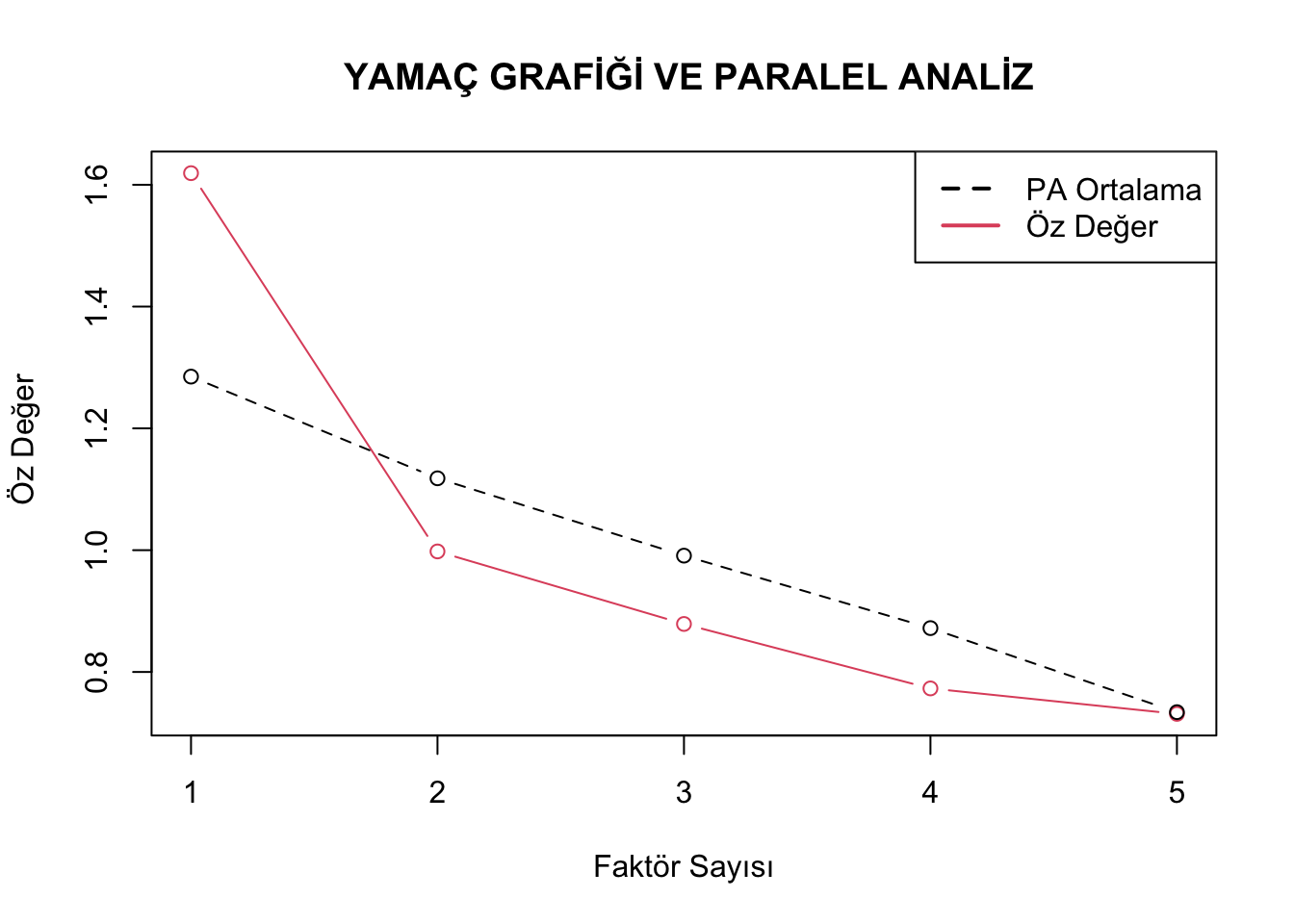

Grafik incelendiğinde paralel analiz sonucunda tek faktörlü bir yapının olduğu görülmektedir. Bu nedenle herhangi bir faktör döndürme işlemine gerek yoktur. Diğer adımlar önceki örneklerle benzer olduğu için burada örneklendirilmemiştir.