3.1 Madde Tepki Kuramı ve Kavramsal Çerçevesi
Önceki bölümde ele aldığımız Klasik Test Kuramı (KTK) belirli sınırlılıklara sahiptir. Bunların başında bireylerin yetenek düzeylerinin uygulanan teste, madde parametrelerinin ise testin uygulandığı gruba bağlı olmasıdır. Başka bir ifade ile kestirilen madde parametreleri (ör: güçlük ve ayırtedicilik indeksleri) testin uygulandığı gruba göre farklılaşabilir.
Benzer şekilde bireylerin ölçülen yetenek düzeyleri de aynı özelliği ölçen farklı testlere göre değişiklik gösterebilir. Örneğin bireyler zor testlerde daha düşük puan alırken kolay testlerde daha yüksek puan alabilirler. Bu durum KTK’da parametre değişmezliğinin sağlanmamasından kaynaklanmaktadır.
Gerçi testin uygulandığı grupların çok farklı olmadığı (aynı evrenden yansız bir şekilde seçilmiş ve yeterli büyüklükte olduğu) veya gruplara uygulanan testlerin içerikleri ve özellikleri çok benzer olduğu durumlarda KTK’nın da parametre değişmezliğinin sağlandığı belirtilebilir (Demars, 2010; Fan, 1998). Ancak pratik anlamda bu koşulların sağlanması her zaman mümkün olmamaktadır.
Klasik test kuramının bir diğer sınırlılığı ölçmenin standart hatasının hesaplanma yaklaşımıdır. KTK’da ölçmenin standart hatası gözlenen puan varyansının gerçek puan varyansının hata ile toplamına eşit olduğu varsayımı üzerine hesaplanır. Standart hata yukarıda belirtilen yaklaşıma dayalı olarak tanımlandığında gözlenen puandan bağımsız olarak hesaplanır. Başka bir ifade ile testi alan tüm bireyler için tek bir standart hata kestirilir.

Klasik test kuramının belirtilen sınırlılıklarının önüne geçmek için ölçme süreci farklı bir bakış açısı ile ele alınmış ve Madde Tepki Kuramı (MTK) olarak adlandırılan yeni bir ölçme kuramı geliştirilmiştir.
MTK yukarıda belirtilen ve KTK’nın çözüm bulamadığı ölçme sorunlarına çözüm getirme iddiasındadır. Bunların başında madde ve birey parametrelerinin değişmezliği varsayımı gelir. Madde Tepki Kuramı (MTK) madde parametrelerinin testin uygulandığı gruptan bağımsız hale getirilebileceği iddiasını taşır. Bu bağlamda MTK farklı testleri eşitleme veya bilgisayarda bireye uyarlanmış testlerin geliştirilmesi gibi bir takım sorunların çözümüne katkı sağlar (Hambleton, Swaminathan & Rogers. 1991). Bunun yanı sıra birey yeteneklerini de testten bağımsız hale getirdiği için MTK temelli geliştirilmiş testler kullanıldığında katılımcıların performansları farklı testler arasında karşılaştırılabilir hale gelir.
MTK’nın KTK’dan temel farklılığı maddeye verilen tepkiler ile birey yeteneği arasında bir ilişki kurmasıdır (Demars,2010). Bu bağlamda MTK’nın dayandığı en temel varsayımlardan birisi, bireyin madde performansı ile madde performansının altında yatan özellik kümesi arasındaki ilişkinin madde karakteristik eğrisi (MKE) olarak adlandırılan monotonik artan bir fonksiyon ile ifade edilebilmesidir.(Hambelton & Swaminathan, 1985; Erkuş vd, 2020). Bu yapısıyla MTK güçlü matematiksel modeller oluşturarak KTK’nın yukarıda bahsedilen sınırlılıklarını aşma iddiasındadır. Adından da anlaşabileceği gibi MTK testten ziyade maddeye odaklanan bir kuramdır.
3.1.1 Madde Karakteristik Eğirisi
Madde karakteristik eğrisi testi alan bireyin sahip olduğu yetenek düzeyine göre maddelerin doğru yanıtlanma olasılıklarını gösteren bir grafiktir. Madde karakteristik eğrisi (MKE) madde puanlarının yordayıcı, yeteneğin ise yordanan değişken olduğu bir regresyon modeli gibi düşünülebilir. Başka bir ifadeyle MKE madde puanlarının test ile ölçülen gizil yapı (yetenek) üzerindeki doğrusal olmayan bir regresyonudur (Aligina & Crocker, 1986). MKE belirli bir yetenek düzeyi aralığındaki bireylerin ( örneğin -3 ve +3 arasındaki) belirli bir maddeyi doğru cevaplama olasılıklarını monotonik olarak artan bir fonksiyon şeklinde ifade eden iki boyutlu bir çizgi grafiğidir. Aşağıda örnek bir madde karakteristik eğrisi verilmiştir.
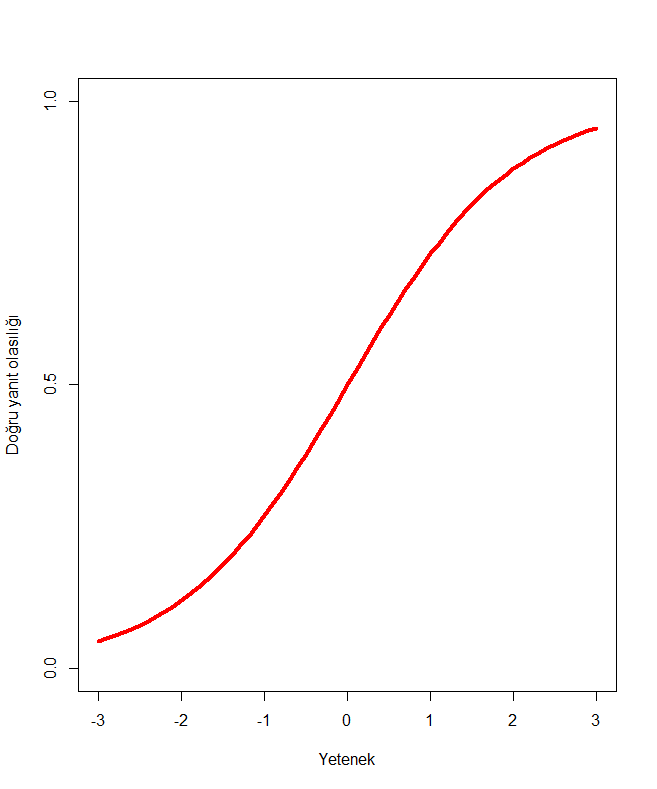
Yukarıdaki verilen şekilde görüldüğü gibi dikey eksen (y ekseni) maddelerin doğru yanıtlanma olasılığını yatay eksen (x ekseni) ise bireylerin yetenek düzeylerini göstermektedir. Madde karakteristik eğrisi, fonksiyonda yer alan parametrelere (madde güçlüğü, madde ayırt ediciliği ve maddenin şansla doğru yanıtlanma olasılığı vb.) göre farklılık gösterir. Fonksiyonda hangi parametrelerin nasıl yer alacağı MTK modellerini oluşturur.
Aşağıda madde karakteristik eğrisini incelemenize olanak verecek bir R Shiny uygulaması bulunmaktadır. Bu uygulamada yer alan madde güçlük parametresi yer almaktadır. Üst tarafta yer alan kaydırma çubuğunun değerlerini değiştirerek MKE’de gerçekleşen değişimleri inceleyebilirsiniz. MKE’yi ekranda net görmek için sağ taraftaki kaydırma çubuğunu aşağı çekebilirsiniz.
Madde tepki kuramının (bu bölümünde tek boyutlu MTK ele alınmıştır ve “MTK” kısaltması veya “Madde Tepki Kuramı” ifadesi ile tek boyutlu madde tepki kuramı ifade edilmiştir) kullanılabilmesi için veri setimizin bazı sayıltıları (varsayımları) karşılaması gereklidir. Bu varsayımlar ana hatları ile aşağıda açıklanmıştır.
3.1.2 Tekboyutluluk
Testi alan bireylerin maddeler üzerindeki performanslarını etkileyen sadece tek bir yetenek türünün olması tekboyutluluk olarak tanımlanabilir (Lord, 1980). Tekboyutluluk, maddeleri bir arada tutan tek ortak bir özelliğin olması veya maddelerin tek bir faktör altında toplanması şeklinde de ifade edilebilir (Crocker & Algina, 1986 ; Erkuş vd, 2020). Bir maddenin doğru cevaplanma olasılığı üzerinde etkili olan birden fazla etmen varsa tekboyutluluğun ihlal edildiği düşünülebilir. Ancak pratikte bunu kusursuz bir şekilde sağlamak çok mümkün değildir. Örneğin uzun sözel ifadeler içeren bir matematik sorusunun doğru yanıtlanma olasılığı üzerinde ilgili matematik yeteneğinin yanı sıra okuduğunu anlama becerisi de etkili olabilir. Eğitimde ve psikoloji alanında ölçmeye konu olan özellikler çoğunlukla karmaşık bir yapıya sahiptir. MTK’nın en çok eleştiri alan kısmı bu varsayımının tam olarak karşılanmasının mümkün olmamasıdır.
Yine de yapılan boyutluluk analizi sonrasında diğer boyutlara kıyasla baskın tek bir boyut söz konusu ise tek boyutluluk varsayımının karşılandığı ifade edilir. Tekboyutluluğun belirlenmesinde faktör analizi neticesinde elde edilen öz değerlerin büyüklüğü veya bu öz değerlerin simülasyon sonucu elde edilen değerlerin ortalaması ile karşılaştırılma sonuçları (Paralel Analiz) dikkate alınır. Aşağıda verilen R Shiny uygulamasını kullanarak veri setinizi (sav uzantılı-SPSS) yükleyip boyutluluk analiz sonuçlarını çıktı olarak elde edebilirsiniz.
1- Öncelikli olarak yükleyeceğiniz veri türünü seçiniz. Veriniz 1-0 gibi ikili puanlanan bir yapıya sahip olabilir veya Likert tipi ölçekler gibi çoklu puanlanan bir yapıya sahip olabilir. Bu ayrım hesaplamalarda arka planda oluşturulacak korelasyon matrisinin yapısının doğru belirlenmesini sağlayacaktır.
2- Çıktı olarak hem öz değer hem de paralel analiz sonuçlarını veren bir grafik yer alacaktır. Paralel analiz sürecinde ön tanımlı olarak 200 tekrar yapılmaktadır.
3- Eğer çıktı da ilk faktör baskın bir yapıya sahipse tek boyutluluk varsayımının sağlandığına ilişkin kanıt elde edebilirsiniz.
3.1.3 Yerel Bağımsızlık
Tekboyutluluk ile kısmen bağlantılı sayılabilecek bir diğer varsayım ise yerel bağımsızlıktır. Yerel bağımsızlık ana hatları ile test performansı üzerinde etkili olan yetenek kontrol edildiğinde (sabit tutulduğunda) bireylerin maddelere vereceği yanıtların (tepkilerin) bağımsız olmasıdır (Reckase, 2009). Yerel bağımsızlık daha basit bir ifade ile testte yer alan bir maddenin başka bir maddenin doğru yanıtlanma olasılığı üzerinde bir etkisinin olmaması şeklinde ifade edilebilir. Tekboyutluluk yerel bağımsızlık ile ilişkilidir çünkü yerel bağımsızlığın sağlanması için tekboyutluluğun sağlanması ön koşulu vardır. Ancak bu durum tekboyutluluk sağlandı diye yerel bağımsızlığın da sağlandığı kabulünü yapmamızı gerektirmez. Erkuş,vd (2020)’de vurgulandığı gibi tek boyutluluk varsayımının sağlanması sürecinde maddeler arası ilişkinin olması herhangi bir yetenek kısıtlamasının olmadığı durumda beklenir. Yerel bağımsızlıkta ise maddeler arası ilişki belirli bir yetenek koşulu altında ele alınmaktadır. Diğer bir ifade ile aynı yapıyı ölçen bir testte maddeler arası ilişki olması beklenen ve istenilen bir durumdur ancak yerel bağımsızlıkta ölçülmek istenen özelliğin sabit tutulması söz konusudur. Yerel bağımsızlığın test edilmesi sürecin de Yen’in Q3 istatistiği kullanılır.
Aşağıda yerel bağımsızlığın testi için hesaplanan Yen’in Q3 istatistiğini hesaplayan basit bir shiny uygulaması bulunmaktadır. Bu uygulamayı kullanmak için;
1- Uzantısı sav (SPSS) olan bir veri setini “veri yükle” kısmını tıklayarak yükleyiniz. Yükleme başarılı bir şekilde tamamlanmış ise ekranda bu belirtilecektir.
2 - Eğer aralarındaki Q3 istatistiği kesme puanı olarak belirlenen 0.37 değerinden yüksek olan maddeler varsa ekrandaki tabloda bu maddeler ve Q3 değerleri gözükecektir.
3- Eğer kesme değeri 0.37’den büyük değere sahip olan maddeler yoksa tablo boş gözükecek ve altında Yerel Bağımsızlığı bozan maddelerin olmadığına ilişkin bir uyarı belirecektir.
MTK modelleri sahip olduğu fonksiyonun türüne göre lojistik ve ogive olmak üzere iki farklı modele sahiptir. Ancak pratikte sağladığı avantajlar ve hesaplanmasının daha kolay olması gerekçesi ile biz lojistik modeller üzerinde duracağız.