2.3 Tek Uygulamaya Dayalı Güvenirlik Belirleme Yöntemleri

Pratik nedenlerden dolayı iki farklı uygulama yapmak pek çok zaman mümkün olamamaktadır. Paralel formların oluşturulmasının zor olması, aynı gruba farklı zamanlarda birden fazla kere ulaşmanın mümkün olmaması, araştırma bütçesinin kısıtlılığı veya zaman darlığı gibi nedenlerle benzer varsayımları temel alan tek uygulamaya dayalı güvenirlik belirleme yöntemleri geliştirilmiştir. Tek uygulamaya dayalı bu yöntemlerde hedef ölçme aracı hedef gruba sadece bir kez uygulanır ve testin kendi içindeki tutarlılığı hesaplanır. Bu nedenle bu yöntem ile elde edilen değerler “iç tutarlık katsayısı” olarak adlandırılır.

İç tutarlık belirleme yöntemlerinin bir kısmı testi iki yarıya bölmeye odaklanırken bazıları madde kovaryanslarına dayalı olarak hesaplanmaktadır. Bu yöntemler arasından yaygın olarak kullanılan “iki yarı güvenirlik katsayısı”, “Kuder-Richardson katsayısı”,“Cronbach-Alpha katsayısı” ve “Hoyt’un Varyans Analizi” ele alınmıştır.

İki-Yarı Güvenirlik Katsayısı İki-yarı güvenirlik katsayısı aynı yapıyı ölçen bir testin iki eşit bölüme ayrılmasını ve her bölümün bir öğrenci grubuna eş zamanlı uygulamasını içerir. İki-yarı güvenirlik katsayının hesaplanabilmesi için testin iki yarısının paralel olduğu yani ortalama ve varyanslarının eşit olduğu varsayımı vardır. Bu varsayımın zarar görmemesi için testin hangi yolla iki yarıya ayrılacağı önem teşkil etmektedir.

Örneğin 50 soruluk bir testi ilk 25 soru birinci yarı son 25 soru ise ikinci yarı olacak şekilde iki yarıya ayrıldığını düşünelim. Birinci olarak bir başarı testinde ilk soruların diğer sorulara göre daha kolay olması durumunda testin ikinci yarısı birinci yarısına göre daha zor olacaktır. Ayrıca öğrenciler testin ilk yarısını daha önce yanıtlayacakları için ikinci yarısının özellikle son sorularını yanıtlarken yorgunluk etkisiyle performans kaybı yaşayabilirler. Bu etmenler testin iki yarısının eşdeğer olması önünde önemli bir engel teşkil eder.

Bu nedenle yaygın olarak kullanılan yöntemlerden biri testin madde numarasının tek-çift olmasına göre testi iki yarıya ayırmaktır. Diğer bir yöntem ise test sorularının seçkisiz olarak ikiye ayırmaktır. Ancak bu yöntemin etkili olabilmesi için soru sayısının az olmaması gerekmektedir. Örneğin 100 soruluk bir test seçkisiz olarak ikiye bölündüğünde her iki yarının birbirine eşdeğer olma olasılığı yüksektir. Ancak 10 soruluk bir test seçkisiz olarak ikiye bölündüğünde iki yarının birbirine eşit olma olasılığı düşük olacaktır ve bu durumda her iki yarının ortalaması ve varyansı farklılaşacaktır. Aşağıda ikiyarı güvenirlik katsayısının matematiksel gösterimi sunulmuştur.

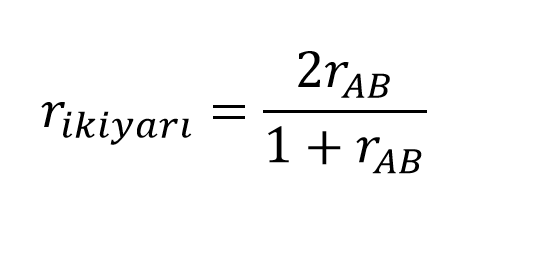
Aşağıda “ltm” paketinde yer alan “LSAT” veri seti kullanılarak “data1” isimli yeni bir veri seti oluşturulmuştur.

dim(data1)
## [1] 100  20

Şimdi “data1” isimli veri seti üzerinden testi iki yarıya bölme yöntemlerini kullanarak iki-yarı güvenirlik katsayısını hesaplayalım. Bu örnekte kullandığımız “data1” isimli veri seti “1-0” şeklinde puanlanan 20 çoktan seçmeli soruya 100 kişinin verdiği yanıtları içermektedir. Öncelikli olarak “tek-çift” yöntemine dayalı olarak testi iki yarıya ayıralım.

tek<-data1[ , seq(1,20 , 2)]
  
cift<-data1[ , seq(2 ,20 , 2)]

head(tek,2)
##   soru 1 soru 3 soru 5 soru 7 soru 9 soru 11 soru 13 soru 15 soru 17 soru 19
## 1      0      0      0      0      1       1       0       1       1       1
## 2      0      0      0      0      1       1       0       1       1       1
head(cift,2)
##   soru 2 soru 4 soru 6 soru 8 soru 10 soru 12 soru 14 soru 16 soru 18 soru 20
## 1      0      0      1      0       1       1       0       1       1       0
## 2      0      0      1      0       1       1       0       1       1       0

Akabinde oluşturduğumuz 2 test için satır toplamlarını hesaplayalım.

top_tek<-rowSums(tek)

top_cift<-rowSums(cift)

Son olarak iki yarı arasındaki korelasyonu hesaplayalıp 2 ile çarpalım (testi iki yarıya ayırdğımız için) ve elde ettiğimiz sonucu korelasyon katsayısının 1 ile toplamına bölelim.

kor<-cor(top_tek,top_cift)

r<-2*kor / (1+kor)

print(r)
## [1] 0.2407665

Aşağıda “tek çift” ve “seçkisiz ayırma” yöntemlerini kullanılarak iki yarı güvenirlik katsayısının hesaplanabileceği bir fonksiyon verilmiştir.

iki.yari<-function(data,yontem="tekcift") {
  tekcift<-function(data) {
    uzunluk<-ncol(data)
    colnames(data)<-1:uzunluk
    bir<-data[,seq(1,uzunluk,2)]
    iki<-data[,seq(2,uzunluk,2)]
    list(bir,iki)
  }
  rastgele<-function(data) {
    n<-ncol(data)
    colnames(data)<- paste0("soru",1:n)
    nn<-n/2
    x1<-colnames(data)
    
    ifelse(n%%2 == 0, s1<-sample(x1,nn),
           s1<-sample(x1,(n+1)/2))
    s2<-which(!x1  %in%  s1)
    bir<- data[, s1]
    iki<- data[, s2]
    list(bir,iki)
  }
if(yontem=="tekcift"){ yari<-tekcift(data)}
if(yontem=="seckisiz") { yari<-rastgele(data)}
sum1<-rowSums(yari[[1]])
sum2<-rowSums(yari[[2]])
kor<-cor(sum1,sum2)
sonuc<- (2*kor) / (1 + kor)
sonuc<-data.frame(rsb=sonuc)
return(sonuc)
}

Bu fonksiyonun ilk girdisi (data) bir matris gerektirmektedir. İkinci girdisi “yontem” ise yontem="tekcift" şeklinde kullanılırsa “tek-çift” yontem="seckisiz" şeklinde kullanılırsa “seçkisiz ayırma” yöntemine dayalı olarak iki yarı güvenirlik katsayısı hesaplanacaktır.

iki.yari(data1, yontem = "tekcift") # Tek çift Yöntemi
##         rsb
## 1 0.2407665
iki.yari(data1, yontem = "seckisiz") # Seçkisiz ayırma yöntemi
##         rsb
## 1 0.6810309

Dikkatinizi çektiği gibi her iki yöntem birbirinden farklı sonuçlar vermiştir. Hatta “seçkisiz ayırma” yöntemi eğer bir sabitleme işlemi yapılmazsa her seferinde testi farklı şekillerde ikiye ayıracağı için her seferinde farklı sonuçlar üretebilecektir (özellikle madde sayısının seçkisiz ayırma için yeterli büyüklükte olmadığı durumlarda).

Bu durumun önüne geçmek için yapılabilecek işlemlerden bir tanesi testi seçkisiz olarak çok defa (örneğin 5000 kez) iki yarıya bölmek, her biri için iki yarı güvenirlik katsayısını hesaplamak ve en sonunda elde edilen iki-yarı güvenirlik katsayılarının ortalamasını almaktır. Şimdi bu durumu örneklendirelim.

Bunun için öncelikle replicate fonksiyonundan faydalanalım. replicate fonksiyonu belirlenen bir işlemin istenilen sayıda tekrar edilmesine olanak sağlar. İlk girdisi tekrar sayısıdır (R=2000). İkinci girdi olarak (FUN) tanımlanmış bir fonksiyon gerektirir. Bu örnekte az önce iki-yarı güvenirlik katsayısı hesaplamak için oluşturduğumuz iki.yari isimli fonksiyon ikinci girdi olarak kullanılmıştır (FUN=iki.yari(data1,"seckisiz).

ikiyari_tekrar <- replicate(5000, iki.yari(data1,yontem="seckisiz"))
rsb<-NULL
for ( i in 1:5000) { rsb[i]<-ikiyari_tekrar[[i]]}
mean(rsb)
## [1] 0.3896484

Bu örnekte seckisiz olarak yarıya bölme işlemi 5000 kere tekrar edilip iki-yarı güvenirlik katsayıları hesaplanmıştır. Elde edilen sonuç ikiyari.tekrar isimli bir obje içerisine aktarılmıştır. İşlem sonucunda obje liste yapısına dönüştüğü için for döngüsü ile listedeki değerler rsb isimli bir vektör içerisine kaydedilmiş ve son olarak bu değerlerin ortalaması alınmıştır. Elde edilen değer replikasyon içermeyen yani tekrar işlemi yapmadan hesapladığımız iki yarı güvenirlik katsayısından daha farklıdır.

Aşağıda iki-yarı güvenirlik katsayısı hesaplamada kullanabileceğiniz bir R Shiny uygulaması bulunmaktadır. Bu uygulama önce testi tek-çift olarak iki yarıya bölerek iki yarı güvenirlik katsayısını hesaplar. Sonrasında ise kullanıcı tarafından belirlenen sayıda testi rastgele olarak ikiye böler ve her koşul için iki yarı güvenirlik katsayısını hesaplar. Akabinde hesaplanan güvenirlik katsayılarının ortalamasını alarak çıktı olarak sunar.

Bu uygulamanın kullanılabilmesi için;

  1. Veri yükleme butonundan “sav” uzantılı (SPSS) bir dosya yükleyiniz.

  2. Seçkisiz olarak iki yarı bölme yöntemi için testin kaç farklı defa iki yarısının oluşturulacağı sayıyı seçiniz.

  3. Çıktıda tek-çift ve seçkisiz ayırma yöntemleri ile elde edilen iki yarı güvenirlik katsayıları ve seçkisiz ayırma yöntemi için kullanılan rastgele bölünme sayısı bulunmaktadır. Shiny uygulamasının bulunduğu pencerenin sağ tarafında bulunan çubuğu aşağı çekerek analiz sonuçlarını görebilirsiniz.

Kuder-Richardson Güvenirlik Katsayısı

KR 20 ve KR 21 formülleri 1-0 şeklinde puanlanan veri türleri için iç tutarlık katsayısını hesaplanmasında kullanılan yöntemlerdir. İki formülü birbirinden ayıran temel nokta testte yer alan maddelerin güçlük düzeylerinin birbirlerine yakın olup olmamasıdır. Eğer testte yer alan maddelerin güçlük düzeyleri aşağı yukarı birbirine eşitse KR21 güvenirlik katsayısı kullanılır.

Aslında testlerin güçlük düzeylerinin eşit olduğu durumlarda KR-20 ve KR-21 çok benzer sonuçlar verirler. Ancak testteki maddelerin güçlük düzeyleri farklılaştığı zaman KR-20 formülü KR-21’e kıyasla daha düşük değerler alır. Bu nedenle KR-20 formülü daha sık kullanılır. Burada KR-20 formülü üzerinde durulmuştur.

Aşağıda KR-20 güvenirlik katsayısının hesaplanmasında bir r fonksiyonu aşağıda tanımlanmıştır.

KR20<-function(x) {
   n<-ncol(x)
  pq<-function(x) { 
    p<-mean(x)
    q<-1-p
     res<-p*q 
    return (res)
     }
pay<- sum(apply(x,2,pq))
top<-rowSums(x)
payda<-var(top)
  result<- n /(n-1)* (1-(pay/payda))
  return(result)
}

Şimdi bu fonksiyonu kullanarak daha önce ele aldığımız “data1” isimli veri seti için KR-20 güvenirlik katsayısını hesaplayalım.

KR20(data1)
## [1] 0.3849119

Dikkatinizi çekebileceği gibi elde edilen sonuç, 5000 tekrar içerecek şekilde hesapladığımız iki yarı güvenirlik katsayısı ile çok yakın bir değer elde edilmiştir. 0 ile 1 arasında değişken KR-20 güvenirlik katsayısı 1’e yaklaştıkça testin iç tutarlılığının daha yüksek olduğu şeklinde yorumlanır. İç tutarlık katsayısı yüksek bir test için ve standart testler için KR-20 katsayısının 0.80 ve üzeri değerler alması beklenir.

Aşağıda KR20 güvenirlik katsayısının hesaplanmasında kullanılabilecek bir R shiny uygulaması bulunmaktadır. Bu uygulamanın kullanılabilmesi için;

  1. Veri yükleme butonundan “sav” uzantılı (SPSS) 1-0 şeklinde puanlanmış bir dosya yükleyiniz.
  2. Çıktıda KR20 katsayısı, kişi sayısı ve madde sayısı yer almaktadır.

Cronbach Alpha Güvenirlik Katsayısı

Cronbach Alpha katsayısı Kuder-Richardson fomulünün çok puanlanan maddelere de uygulanacak şekilde geliştirilmiş halidir. Bu nedenle KR-20 formülüne oldukça benzer. En önemli farklılığı varyansın hesaplanma biçimidir. KR-20 1-0 şeklinde puanlanan testlere uygulandığı için madde varyansı “pq” ( yani maddenin doğru yanıtlanma oranının yanlış yanıtlanma oranı ile çarpımı) şeklinde hesaplanır. Cronbach Alpha ise ham puanların ortalama puanlardan sapmasına dayalı bildiğimiz varyans hesaplaması kullanılır. Bu bağlamda Cronbach Alpha katsayısı hem 1-0 şeklinde puanlanan (ör.çoktan şeçmeli) hem de çoklu puanlanan (ör. Likert tipi ölçekler) testlerin iç tutarlılığın hesaplanmasında yaygın kullanılan bir yöntemdir. Aslında Cronbach alpha katsayısı Guttman tarafından daha önce geliştirilmiştir. Cronbach bu formülü gündeme getirmiş ve yaygın kullanılmasına önayak olmuştur. Bu nedenle bazı kaynaklarda formülün asıl isminin “Guttman-Cronbach Alpha Katsayısı” olması gerektiği belirtilir (Erkuş & vd.2020; Sijtsma, 2009; McDanold, 1999). Aşağıda Cronbach Alpha katsayısının matamatiksel gösterimi sunulmuştur.

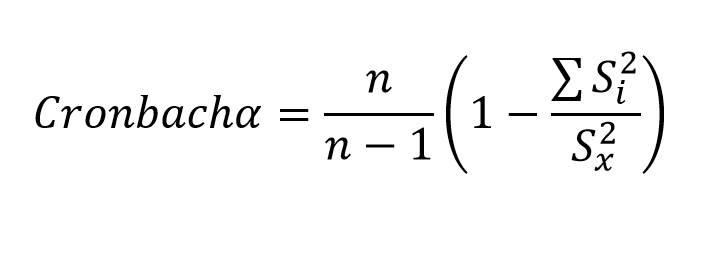
Cronbach Alpha’nın en sık kullanılan iç tutarlık belirleme yöntemi olduğu söylenebilir. Bu bağlamda “psych” (Revelle, 2019), “psy” (Falissard, 2012),“ltm” (Rizopoulos, 2006), “validateR” gibi pekçok paket bu katsayının hesaplanmasında kullanılacak fonksiyonlar içermektedir. “validateR” paketi CRAN ortamında bulunmadığı için devtools::install_github(repo= "cddesja/validateR") kodunu çalıştırmanız gerekmektedir. Ancak daha kapsamlı olduğu için biz “psych” ve “ltm” paketi üzerinden örneklendirme yapacağız.

install.packages("psych") ; library(psych)
install.packages("tlm") ;  library(ltm) 
cronbach.alpha(LSAT)
## 
## Cronbach's alpha for the 'LSAT' data-set
## 
## Items: 5
## Sample units: 1000
## alpha: 0.295

Benzer şekilde psych paketinde yer alan alpha fonksiyonu ile de Cronbach Alpha iç tutarlılık katsayısı hesaplanabilir ancak bu fonksiyon daha ayrıntılı bir çıkıya sahiptir.

alpha(LSAT)
## 
## Reliability analysis   
## Call: alpha(x = LSAT)
## 
##   raw_alpha std.alpha G6(smc) average_r  S/N   ase mean   sd median_r
##       0.29      0.29    0.25     0.077 0.41 0.034 0.76 0.21     0.08
## 
##     95% confidence boundaries 
##          lower alpha upper
## Feldt     0.22  0.29  0.36
## Duhachek  0.23  0.29  0.36
## 
##  Reliability if an item is dropped:
##        raw_alpha std.alpha G6(smc) average_r  S/N alpha se   var.r med.r
## Item 1      0.28      0.28    0.22     0.087 0.38    0.037 0.00063 0.093
## Item 2      0.24      0.24    0.19     0.071 0.31    0.038 0.00126 0.076
## Item 3      0.22      0.22    0.17     0.065 0.28    0.039 0.00077 0.068
## Item 4      0.25      0.25    0.20     0.075 0.32    0.037 0.00108 0.080
## Item 5      0.27      0.27    0.22     0.084 0.37    0.037 0.00079 0.086
## 
##  Item statistics 
##           n raw.r std.r r.cor r.drop mean   sd
## Item 1 1000  0.36  0.49  0.20   0.11 0.92 0.27
## Item 2 1000  0.57  0.52  0.28   0.15 0.71 0.45
## Item 3 1000  0.62  0.54  0.32   0.17 0.55 0.50
## Item 4 1000  0.53  0.51  0.26   0.14 0.76 0.43
## Item 5 1000  0.44  0.49  0.22   0.12 0.87 0.34
## 
## Non missing response frequency for each item
##           0    1 miss
## Item 1 0.08 0.92    0
## Item 2 0.29 0.71    0
## Item 3 0.45 0.55    0
## Item 4 0.24 0.76    0
## Item 5 0.13 0.87    0

Çıktıda görüldüğü gibi alpha fonksiyonu ek olarak maddeler testten çıkartıldığı zaman güvenirlik katsayısında gerçekleşen değişim ve madde istatistikleri de sunulur. Bu paketin en önemli özelliklerinden birisi de “bootstrap” yöntemi ile oluşturulan yeni örneklemler için hesaplanan Cronbach Alpha katsayılarının dağılımının elde edilmesi ve güven aralıklarının hesaplanabilmesidir. Bunun için n.iter argümanı kullanılır. Ön tanımlı olarak bu argüman n.iter=1 şeklinde belirlenmiştir.

alpha(LSAT,n.iter = 2000)
## 
## Reliability analysis   
## Call: alpha(x = LSAT, n.iter = 2000)
## 
##   raw_alpha std.alpha G6(smc) average_r  S/N   ase mean   sd median_r
##       0.29      0.29    0.25     0.077 0.41 0.034 0.76 0.21     0.08
## 
##     95% confidence boundaries 
##              lower alpha upper
## Feldt         0.22  0.29  0.36
## Duhachek      0.23  0.29  0.36
## bootstrapped  0.22  0.30  0.36
## 
##  Reliability if an item is dropped:
##        raw_alpha std.alpha G6(smc) average_r  S/N alpha se   var.r med.r
## Item 1      0.28      0.28    0.22     0.087 0.38    0.037 0.00063 0.093
## Item 2      0.24      0.24    0.19     0.071 0.31    0.038 0.00126 0.076
## Item 3      0.22      0.22    0.17     0.065 0.28    0.039 0.00077 0.068
## Item 4      0.25      0.25    0.20     0.075 0.32    0.037 0.00108 0.080
## Item 5      0.27      0.27    0.22     0.084 0.37    0.037 0.00079 0.086
## 
##  Item statistics 
##           n raw.r std.r r.cor r.drop mean   sd
## Item 1 1000  0.36  0.49  0.20   0.11 0.92 0.27
## Item 2 1000  0.57  0.52  0.28   0.15 0.71 0.45
## Item 3 1000  0.62  0.54  0.32   0.17 0.55 0.50
## Item 4 1000  0.53  0.51  0.26   0.14 0.76 0.43
## Item 5 1000  0.44  0.49  0.22   0.12 0.87 0.34
## 
## Non missing response frequency for each item
##           0    1 miss
## Item 1 0.08 0.92    0
## Item 2 0.29 0.71    0
## Item 3 0.45 0.55    0
## Item 4 0.24 0.76    0
## Item 5 0.13 0.87    0

Cronbach Alpha iç tutarlık katsayısının hesaplanması için bir fonksiyon aşağıda tanımlanmıştır.

cr.alpha<- function(data,yontem="kor") {
  
  n<-ncol(data)
  kor<-cor(data)
kor1<-as.vector(kor)
kor2<-unique (kor1)
kor3<- kor2[-1]
kor4<-sum(kor3)/length(kor3)
pay_kor<- n*kor4
payd_kor<- (1 + (n-1)*kor4)
alphakor<-pay_kor/payd_kor
   
   kov<-cov(data)
  kov1<-as.vector(kov)
  kov2<-unique (kov1)
  kov3<- kov2[-1]
  kov4<-sum(kov3)/length(kov3)
  pay_kov<- n*kov4
  payd_kov<- (1 + (n-1)*kov4)
  alphakov<-pay_kov/payd_kov
  
  if( yontem=="kor") { return(alphakor) }
  if (yontem=="kov")  {  return(alphakov)}
}

Yukarıda tanımlanmış olan cr.alpha fonksiyonu iki girdi içermektedir. Bunlardan ilki olandata girdisi hesaplamanın yapılacağı veri setinin adının girilmesini gerektirir. Bu veri matris türünde olmalıdır. İkincisi ise yontemdir ve hesaplanacak Alpha katsayısının korelasyon matrisi mi yoksa kovaryans matrisi mi üzerinden hesaplanacağı belirtilir. Aşağıda “çoklu puanlanan 15 madde ve 400 gözlemden oluşan”LSAT” isimli veri seti üzerinden yapılan hesaplama sonuçları sunulmuştur.

dim(LSAT)
## [1] 1000    5
cr.alpha(data=LSAT,yontem="kor")
## [1] 0.2930283
cr.alpha(data=LSAT,yontem="kov")
## [1] 0.2499092

Aşağıda Cronbach Alpha iç tutarlık katsayısının hesaplanmasında kullanılabilecek bir R Shiny uygulaması sunulmuştur. Bu uygulamanın kullanılabilmesi için aşağıdaki adımlar gerçekleştirilir

  1. Veri yükleme butonundan “sav” uzantılı (SPSS) bir dosya yükleyiniz.

  2. Çıktıda Cronbach Alpha katsayısı, kişi sayısı ve madde sayısı yer almaktadır. Shiny uygulamasının bulunduğu pencerenin sağ tarafında bulunan çubuğu aşağı çekerek analiz sonuçlarını görebilirsiniz.

Hoyt’un Varyans Analizi

Adından da anlaşılacağı gibi varyans üzerinde temellendirilen bu yöntem bireyler ve maddeler arası değişim hakkında bilgi verir (Crocker&Algina, 1986). Hoyt (1941), ölçme sonucuna ilişkin varyansı bireyler arası, maddeler arası ve seçkisiz (rastgele) varyans olmak üzere üç bileşene ayırmıştır. (Akt: Bademci, 2011). Hoyt’un varyans analizi bu yapısı ile genellenebilirlik kuramının gelişimine de katkı sağlamıştır. (Brennan, 1992). 1-0 şeklinde puanlanan testler düşünüldüğünde KR20, Cornbach Alpha ve Hoyt’un varyans analizi yöntemleri çok benzer sonuçlar verir (Bademci, 2011).

Aşağıda Hoyt’un varyans analizi için kullanılabilecek bir R shiny uygulaması sunulmuştur. Bu uygulamayı kullanmak için aşağıdaki adımları izlemeniz gerekmektedir.

  1. Veri yükleme butonundan “sav” uzantılı (SPSS) bir dosya yükleyiniz.

Çıktıda Hoyt’un varyans analizi katsayısı, madde sayısı ve katılımcı sayısı yer almaktadır.