6.4 Parametre Değerlerinin Değerlendirilmesi

Önceki örneklerde gördüğünüz gibi çeşitli parametrelerin (a, b, c) alacağı değerleri belirleyerek simülatif veriler ürettik. Örneğin ürettiğimiz 10 maddelik bir testin belirlediğimiz “b” veya “a” parametrelerine sahip olmasını istedik. Acaba ürettiğimiz veri seti üzerinden parametre kestirimlerini yaparsak elde ettiğimiz değerler veri üretiminden önce belirlediğimiz değerlere ne kadar yakın olacaktır? Bu sorunun yanıtı ürettiğimiz verinin istediğimiz özelliklere ( parametre değerlerine) sahip olup olmadığının bir kanıtı olacaktır.

Bu amaçla “RMSE” ve “Yanlılık” ölçümleri bize yukarıda bahsettiğimiz sorunun yanıtını verecektir. Öncelikli olarak bu üç istatistiği açıklayalım:

RMSE (Root Mean Square Error) kısaltması ile kullandığımız istatistik temelde kestirilen parametre değeri ile gerçek parametre değeri arasındaki farkın karesinin örneklem büyüklüğüne bölümünün kareköküdür. Ancak bu işlem her bir tekrar için yapılmalıdır. Aşağıda RMSE’nin matematiksel gösterimi sunulmuştur.

Ancak kestirilen parametre değerlerinin değerlendirilebilmesi için bu işlemi her bir tekrar (replikasyon) için gerçekleştirip elde ettiğimiz RMSE değerlerinin ortalamasını almamız gerekmektedir. Şimdi örnek bir uygulama üzerinden Rasch modele uygun 20 tekrar içerecek şekilde üretilen veri setleri için gerçek ve kestirilen “b” parametreleri için RSMSE istatistiğini hesaplayalım.

Bunun için öncelikle 50 tekrar içerecek şekilde Rasch Modele uygun veri setleri üretelim. Bunun için daha önce oluşturduğumuz “pl1veri” isimli fonksiyondan faydalanacağız

veriler<-list()
for ( i in 1:50)  {   
  veriler[[i]]<- pl1veri(nitem=5, n=500, a=1, minb = -2, maxb = 2)
}

Bunun için ilk başta üretilen veri setlerini muhafaza edeceğimiz “veriler” isimli boş bir vektör oluşturduk. Akabinde ise “for” döngüsünden faydalanarak “b” parametresi -2 ve 2 değerleri arasında değişen 5 madde 500 yanıtlayıcıdan oluşan Rasch modele uygun 50 veri seti üretip bunları boş liste içerisinde atadık. Rasch modeli olduğu için “a” parametresini “1” değerine sabitledik. Bu veri setinin bir tanesinin ilk 10 satırını örnek olarak sunalım.

veriler[[1]][1:12,]

##             madde1    madde2    madde3    madde4     madde5
## b       -0.8166611 -1.874185 0.2474829 -1.949438 -0.2798453
## a        1.0000000  1.000000 1.0000000  1.000000  1.0000000
## birey1   1.0000000  1.000000 0.0000000  1.000000  1.0000000
## birey2   0.0000000  0.000000 0.0000000  1.000000  1.0000000
## birey3   1.0000000  1.000000 1.0000000  1.000000  1.0000000
## birey4   1.0000000  0.000000 0.0000000  1.000000  1.0000000
## birey5   1.0000000  1.000000 0.0000000  1.000000  0.0000000
## birey6   0.0000000  1.000000 0.0000000  0.000000  0.0000000
## birey7   1.0000000  1.000000 1.0000000  1.000000  1.0000000
## birey8   1.0000000  1.000000 0.0000000  1.000000  0.0000000
## birey9   0.0000000  1.000000 0.0000000  1.000000  0.0000000
## birey10  1.0000000  1.000000 0.0000000  1.000000  1.0000000

Görüldüğü gibi çıktının ilk satırında “b” parametreleri var. İkinci satırında ise “1” değerine sabitlenmiş “a” parametreleri var. Bu yapı üretilen diğer veri setleri için de aynı şekildedir. Çıktılarda görülen bu parametreler veri setlerini üretirken kullandığımız parametrelerdir. Başka bir ifade ile gerçek “b” parametreleridir.

Şimdi bu veri setleri üzerinden b parametresinin kestirimlerini yapmamız gerekmektedir ki gerçek ve kestirilen parametre değerlerini karşılaştırabilelim. Bunun için “mirt” paketinden faydalanacağız. Parametre kestirimlerinin detayı için kitabın ilgili bölümünü (3. Bölüm) incelemenizi öneririz. Burada bu sürece ilişkin ayrıntılı açıklamalara yer verilmemiştir. Tabi ki de bu işlemi ürettiğimiz 50 veri seti için ayrı ayrı yapacağımızdan “for” döngüsünden faydalanmak işimizi oldukça kolaylaştıracaktır.

library(mirt)

uyum<-list()

for ( i in 1:50) {

uyum[[i]] <- mirt(data = veriler[[i]][3:500,], model = 1,
              SE = TRUE, verbose = FALSE, itemtype = "Rasch")
}

kes_param<-list()

for ( i in 1:50) {

    kes_param[[i]]<- coef( uyum[[i]], IRTpars = TRUE, simplify = TRUE)$items
}
kes_param[[20]]

##        a          b g u
## madde1 1 -0.5051197 0 1
## madde2 1  1.6358966 0 1
## madde3 1  0.4176638 0 1
## madde4 1  1.1025321 0 1
## madde5 1 -0.6743209 0 1

Yukarıdaki kodlar ile üretmiş olduğumuz 50 veri seti için “b” parametresinin kestirimini elde ettik ve sonuçları “kes_param” isimli liste içerisine kaydettik. Örnek olarak 20. veri için parametre kestirimleri sunulmuştur. Çıktıda 5 maddeye ilişkin parametre değerleri görülmektedir.

Ürettiğimiz veri setleri için gerçek ve kestirilen parametre değerleri olduğu için “RMSE” hesaplama sürecine geçebiliriz. Bunun için kendi kodlarımızı yazabileceğimiz gibi “Metrics” paketinden de faydalanabiliriz. Bu paket içindeki “rmse” fonksiyonu RMSE hesaplama sürecini pratikleştirecektir.

library(Metrics)
rmseb<-c()
for( i in 1:50) {
rmseb[i]<- rmse( as.numeric( veriler[[i]][1,] ), as.numeric(kes_param[[i]][,2]) ) }
str(rmseb)

##  num [1:50] 0.1415 0.0795 0.1648 0.0708 0.1079 ...

mean(rmseb)

## [1] 0.1222336

Yukarıdaki kodlarda her bir veri seti için ayrı ayrı kestireceğimiz RMSE değerlerini atamak için boş bir vektör oluşturduk rmseb<-c(). Sonrasında “veriler” listesi içerisindeki 50 veri setinin ilk satırında bulunan gerçek “b” parametrelerini veriler[[i]][1,] ve “kes_param” listesi içerisindeki 50 veri seti için kestirilen parametrelerin 2. sütununda bulunan “b” parametrelerini kes_param[[i]][,2]) rmse fonksiyonu içerisinde kullandık rmse(as.numeric( veriler[[i]][1,] ), as.numeric(kes_param[[i]][,2]) ). Tabi ki bu işlemi “for” döngüsü yardımı ile her bir 50 veri seti için ayrı ayrı gerçekleştirdik ve sonuçları “rmseb” isimli vektöre kaydettik. Bu vektör RMSE değerlerini içermektedir. Bu değerlerin ortalamasını alıp ortalama RMSE değerini elde edebiliriz.

Kestirilen parametreleri değerlendirmede kullanılabilecek bir diğer istatistik ise yanlılıktır (bias). Yanlılığın matematiksel gösterimi aşağıdaki gibidir. Yanlılık basit olarak kestirilen ve gerçek parametrelerin farklarının karesine karşılık gelir.

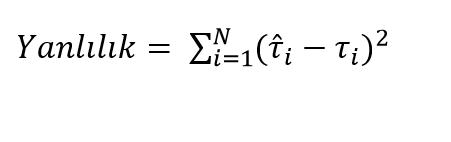
Şimdi RMSE hesapladığımız veri setleri için yanlılık değerini hesaplayalım. Bunun için yine “Metrics” paketi içerisinde yer alan “bias” fonksiyonundan faydalanacağız. Bu fonksiyonda rmse fonksiyonu gibi girdi olarak ve kestirilen parametreleri kullanır.

library(Metrics)
biasb<-c()
for( i in 1:50) {
biasb[i]<- bias( as.numeric( veriler[[i]][1,] ), as.numeric(kes_param[[i]][,2]) ) }
str(biasb)

##  num [1:50] -0.1322 -0.00723 0.07263 0.00773 0.05855 ...

mean(biasb)

## [1] -0.00729007

Burada da RMSE hesaplarken kullandığımız aynı süreçleri takip ettik. Öncelikli olarak “biasb” isimli boş bir vektör oluşturduk. Sonrasında “for” döngüsü ile daha önce içerisine ve kestirilen parametreleri atadığımız listeleri kullanarak yanlılık değerini hesapladık. Son olarak üretilen 50 veri seti için hesaplanan yanlılık değerlerinin ortalaması alınmıştır.

Bu istatistiklerin kullanılan lojistik modele göre farklı parametreler için de hesaplanması gereklidir. Biz burada Rasch modele dayalı veri ürettiğimiz için “b” parametresine odaklandık. Diğer mtk modelleri için “a” ve “c” veya “u” parametreleri için de bu istatistikler hesaplanabilir. Ayrıca modellerden bağımsız olarak gerçek ve kestirilen yetenek kestirimleri de bahsi geçen ve benzer istatstikler için kullanılabilir.