5.3 İkinci düzey DFA ve Yapısal Eşitlik Modellemesi
5.3.1 İkinci Düzey DFA
Şimdiye kadar test edilen DFA modelinde, yalnızca gizil değişkenler ve onların açıklamaya çalıştığı gözlenen değişkenler vardı. Ölçek geliştirme örneği düşünüldüğünde bazen faktörlerden alınan toplam puanlar ayrı ayrı değerlendirilirken, bazen ölçekten toplam bir puan almak istenebilir. Ancak birbirinden bağımsız olan bu iki faktör, toplanabilir mi? Bunu test etmek için DFA modelinde, üst bir gizil değişken tanımlanır ve faktörlerle ilişkilendirilir. Bunu yapmak için modelde aşağıdaki gibi bir düzenleme yapılabilir:
Ancak modelin tanımlı olmasına ilişkin kurallar burada da geçerlidir. Hatırlarsanız üç madde ve bir faktör olduğunda modelin serbestlik derecesi sıfır olduğundan model tam tanımlı oluyordu. İkinci düzey DFA için de en az üç faktörün, üst düzey bir faktör altında yer alması gerekmektedir. Dolayısıyla, örnekteki model tanımsız bir model olacaktır. Yine de analiz adımlarının gösterilmesi ve aynı örneğe bağlı kalınması bakımından analiz çıktılarına yer verilmiştir.Bu model test edildiğinde aşağıdaki gibi bir çıktı vermektedir:
## Warning in lav_model_vcov(lavmodel = lavmodel, lavsamplestats = lavsamplestats, : lavaan WARNING:
## The variance-covariance matrix of the estimated parameters (vcov)
## does not appear to be positive definite! The smallest eigenvalue
## (= -3.629663e-07) is smaller than zero. This may be a symptom that
## the model is not identified.## lavaan 0.6.15 ended normally after 25 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 14
##
## Number of observations 252
##
## Model Test User Model:
## Standard Scaled
## Test Statistic 72.331 58.074
## Degrees of freedom 7 7
## P-value (Chi-square) 0.000 0.000
## Scaling correction factor 1.246
## Yuan-Bentler correction (Mplus variant)
##
## Model Test Baseline Model:
##
## Test statistic 424.192 291.533
## Degrees of freedom 15 15
## P-value 0.000 0.000
## Scaling correction factor 1.455
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.840 0.815
## Tucker-Lewis Index (TLI) 0.658 0.604
##
## Robust Comparative Fit Index (CFI) 0.842
## Robust Tucker-Lewis Index (TLI) 0.661
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -2083.419 -2083.419
## Scaling correction factor 1.232
## for the MLR correction
## Loglikelihood unrestricted model (H1) -2047.254 -2047.254
## Scaling correction factor 1.236
## for the MLR correction
##
## Akaike (AIC) 4194.839 4194.839
## Bayesian (BIC) 4244.251 4244.251
## Sample-size adjusted Bayesian (SABIC) 4199.869 4199.869
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.192 0.170
## 90 Percent confidence interval - lower 0.154 0.135
## 90 Percent confidence interval - upper 0.234 0.207
## P-value H_0: RMSEA <= 0.050 0.000 0.000
## P-value H_0: RMSEA >= 0.080 1.000 1.000
##
## Robust RMSEA 0.190
## 90 Percent confidence interval - lower 0.147
## 90 Percent confidence interval - upper 0.237
## P-value H_0: Robust RMSEA <= 0.050 0.000
## P-value H_0: Robust RMSEA >= 0.080 1.000
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.087 0.087
##
## Parameter Estimates:
##
## Standard errors Sandwich
## Information bread Observed
## Observed information based on Hessian
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Faktor_A =~
## a1 1.000 0.574 0.521
## a2 1.397 0.311 4.488 0.000 0.802 0.735
## a3 1.426 0.297 4.807 0.000 0.819 0.746
## Faktor_B =~
## b1 1.000 0.465 0.449
## b2 1.276 0.220 5.798 0.000 0.593 0.563
## b3 1.791 0.425 4.216 0.000 0.833 0.766
## Genel_Faktor =~
## Faktor_A 1.000 0.926 0.926
## Faktor_B 0.822 0.049 16.915 0.000 0.940 0.940
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .a1 0.888 0.106 8.334 0.000 0.888 0.729
## .a2 0.548 0.114 4.789 0.000 0.548 0.460
## .a3 0.533 0.120 4.456 0.000 0.533 0.443
## .b1 0.859 0.094 9.176 0.000 0.859 0.799
## .b2 0.759 0.116 6.522 0.000 0.759 0.683
## .b3 0.489 0.096 5.114 0.000 0.489 0.413
## .Faktor_A 0.047 0.054 0.873 0.383 0.143 0.143
## .Faktor_B 0.025 0.047 0.533 0.594 0.117 0.117
## Genel_Faktor 0.283 0.088 3.219 0.001 1.000 1.000Bu modele ilişkin yol grafiği ise aşağıdaki gibidir:
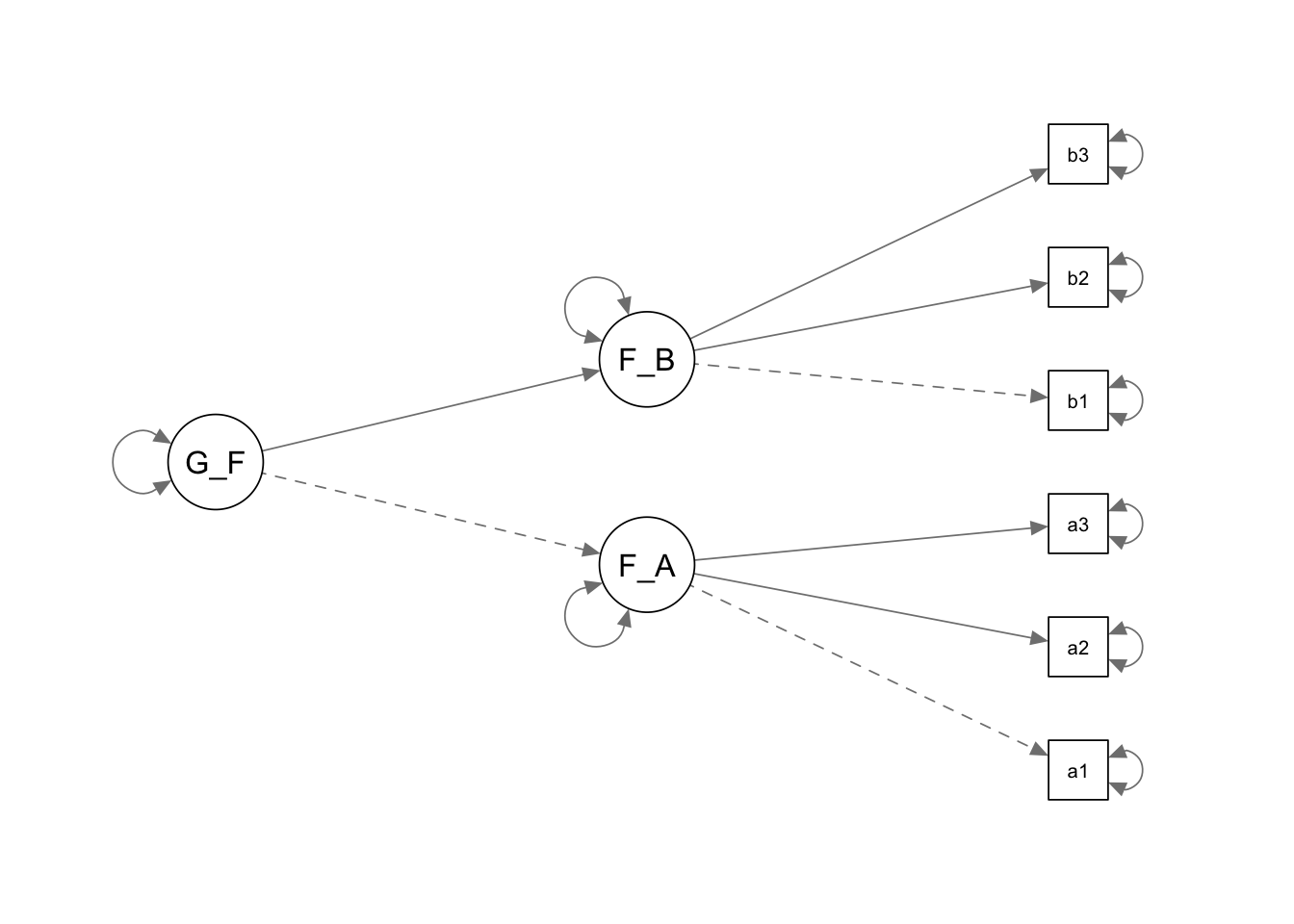
5.3.2 Yapısal Eşitlik Modellemesi
Yapısal eşitlik modellemesi, gizil değişkenler arasındaki ilişkilerin araştırıldığı bir analiz, hatta analiz ailesidir. Yapısal eşitlik modeli çalışmalarında iki model test edilir, bunlar ölçme modeli ve yapısal modeldir. Ölçme modeli DFA ile test edilir ve gözlenen değişkenler ile gizil değişkenler arasındaki ilişkiler araştırılır. Ölçme modelinin doğrulanması halindeyse, gizil değişkenler ilişkilendirilerek yapısal model test edilir.
Yapısal model test edilirken modelde gizil değişkenler arasındaki ilişkiler “~” işareti ile tanımlanır. Regresyon analizinde gözlenen değişkenler (toplam puanlar) arasındaki ilişkilere dayalı bir model kurulurken, YEM’de modele dahil edilen değişkenler gizildir ve gözlenen değişkenlerin altında yatan soyut kavramsal yapılardır. Basit bir YEM modeli aşağıdaki gibi tanımlanıp test edilebilir:
model <- "Faktor_A =~ a1 + a2 + a3
Faktor_B =~ b1 + b2 + b3
Faktor_A ~ Faktor_B"
yem <- sem(model = model, data = veri, estimator = "MLR")
summary(yem, standardized = TRUE, fit.measures = TRUE)## lavaan 0.6.15 ended normally after 31 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 13
##
## Number of observations 252
##
## Model Test User Model:
## Standard Scaled
## Test Statistic 72.331 66.370
## Degrees of freedom 8 8
## P-value (Chi-square) 0.000 0.000
## Scaling correction factor 1.090
## Yuan-Bentler correction (Mplus variant)
##
## Model Test Baseline Model:
##
## Test statistic 424.192 291.533
## Degrees of freedom 15 15
## P-value 0.000 0.000
## Scaling correction factor 1.455
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.843 0.789
## Tucker-Lewis Index (TLI) 0.705 0.604
##
## Robust Comparative Fit Index (CFI) 0.842
## Robust Tucker-Lewis Index (TLI) 0.704
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -2083.419 -2083.419
## Scaling correction factor 1.326
## for the MLR correction
## Loglikelihood unrestricted model (H1) -2047.254 -2047.254
## Scaling correction factor 1.236
## for the MLR correction
##
## Akaike (AIC) 4192.839 4192.839
## Bayesian (BIC) 4238.722 4238.722
## Sample-size adjusted Bayesian (SABIC) 4197.510 4197.510
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.179 0.170
## 90 Percent confidence interval - lower 0.142 0.135
## 90 Percent confidence interval - upper 0.217 0.207
## P-value H_0: RMSEA <= 0.050 0.000 0.000
## P-value H_0: RMSEA >= 0.080 1.000 1.000
##
## Robust RMSEA 0.178
## 90 Percent confidence interval - lower 0.140
## 90 Percent confidence interval - upper 0.218
## P-value H_0: Robust RMSEA <= 0.050 0.000
## P-value H_0: Robust RMSEA >= 0.080 1.000
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.087 0.087
##
## Parameter Estimates:
##
## Standard errors Sandwich
## Information bread Observed
## Observed information based on Hessian
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Faktor_A =~
## a1 1.000 0.574 0.521
## a2 1.397 0.311 4.488 0.000 0.802 0.735
## a3 1.426 0.297 4.807 0.000 0.819 0.746
## Faktor_B =~
## b1 1.000 0.465 0.449
## b2 1.276 0.220 5.798 0.000 0.593 0.563
## b3 1.791 0.425 4.216 0.000 0.833 0.766
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Faktor_A ~
## Faktor_B 1.074 0.234 4.586 0.000 0.870 0.870
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .a1 0.888 0.106 8.334 0.000 0.888 0.729
## .a2 0.548 0.114 4.789 0.000 0.548 0.460
## .a3 0.533 0.120 4.456 0.000 0.533 0.443
## .b1 0.859 0.094 9.176 0.000 0.859 0.799
## .b2 0.759 0.116 6.522 0.000 0.759 0.683
## .b3 0.489 0.096 5.114 0.000 0.489 0.413
## .Faktor_A 0.080 0.036 2.200 0.028 0.243 0.243
## Faktor_B 0.216 0.090 2.410 0.016 1.000 1.000Görülebileceği gibi DFA’dan farklı olarak modeldeki gizil değişkenler ilişkilendirilmiştir. Modelde yapılan Faktor_A ~ Faktor_B tanımlamasında, ok sembolü Faktor_B’den Faktor_A’ya olacak şekilde çizilir ve Faktör_B’nin Faktor_A’yı açıklama düzeyi test edilir. Böyle bir modele ilişkin yol grafiği aşağıda verilmiştir:
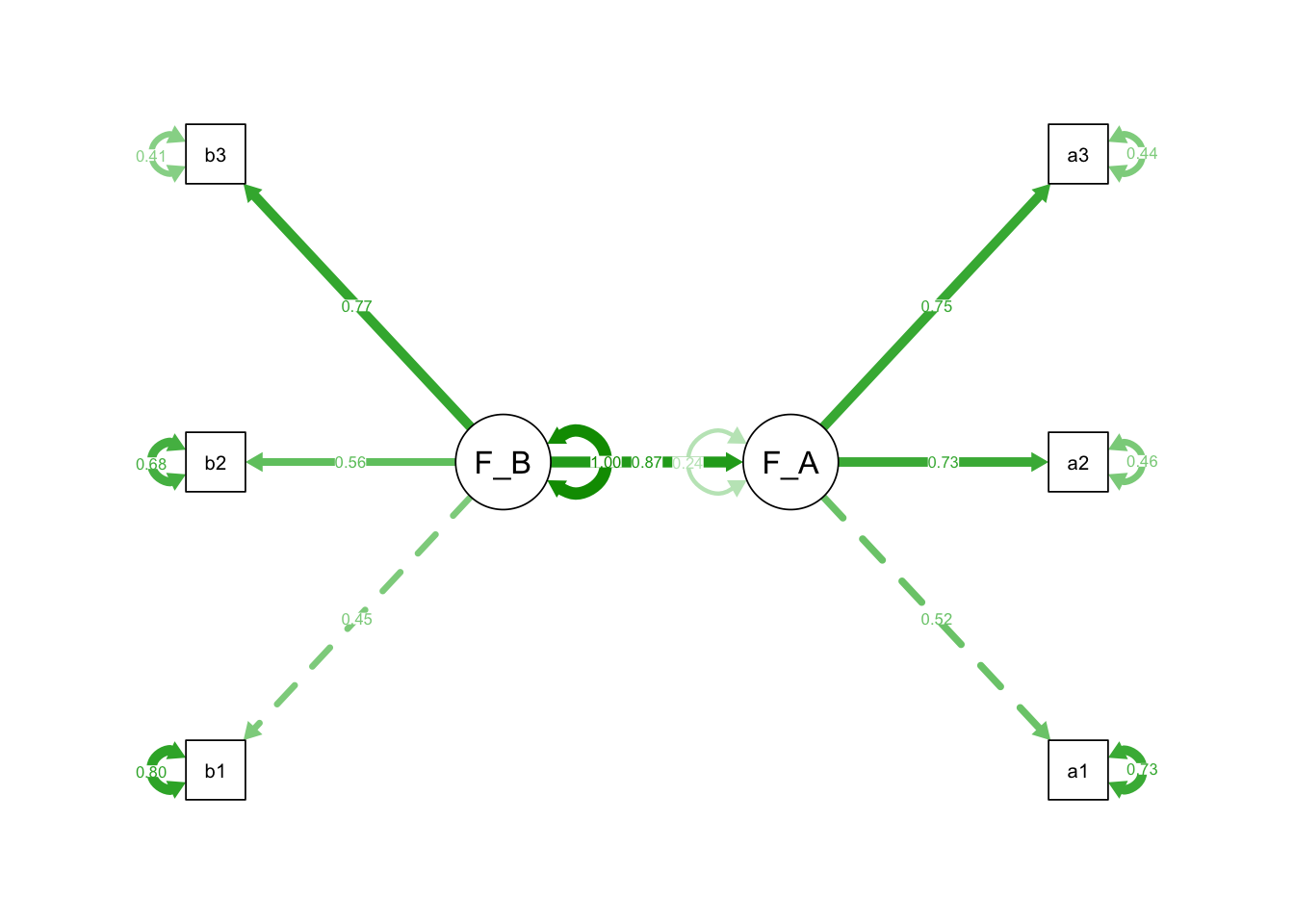
Dikkat edilirse, okun yönü Faktor_B’den Faktor_A’ya doğru çizilmiştir. Ayrıca “semPaths” fonksiyonu içerisinde “what” argümanı “std” olacak şekilde yazılmıştır. Bu nedenle yol grafiğinin rengi yeşil olmuş, ayrıca parametrelere ait standartlaştırılmış faktör yüklerine de yer verilmiştir.
Lavaan paketine ait temel fonksiyonlar bunlardır. Lavaan hakkında daha detaylı bilgi için lavaan paketinin dökümantasyonu incelenebilir. Buna göre aracılık modelleri ve ölçme değişmezliği testleri gerçekleştirilebilir.