4.3 Çoklu Puanlanan Maddeler İçeren bir Ölçek için AFA Hesaplama

Bu bölümde örnek bir veri seti üzerinden “psych” paketi üzerinden AFA hesaplama süreci özetlenmiştir. Daha önce de vurgulandığı gibi AFA sürecinde faktör çıkarma tekniği olarak “Temel Bileşen Analizi” kullanılmıştır. Ancak anlatım kolaylığı sağlaması açısından “AFA” kısaltması kullanılmıştır.

Bu örneğimiz için “mirt” paketinin içerisinde yer alan “SAT12” veri setinden faydalanacağız. Veri setinin orijinalinde 1 ila 8 arasında puanlanan 32 madde bulunmaktadır. Ancak biz bu örneğimizde “SAT12” veri setindeki ilk 10 maddeyi dikkate alacağız. Bu yeni oluşturduğumuz veri setini “ornek_veri” isimli bir obje içerisine kaydettik. Son olarak veri setinin ilk 5 satırı sunulmuştur.

library(mirt)

ornek_veri<- SAT12[,1:10]

head(ornek_veri,5)

##   Item.1 Item.2 Item.3 Item.4 Item.5 Item.6 Item.7 Item.8 Item.9 Item.10
## 1      1      4      5      2      3      1      2      1      3       1
## 2      3      4      2      8      3      3      2      8      3       1
## 3      1      4      5      4      3      2      2      3      3       2
## 4      2      4      4      2      3      3      2      4      3       2
## 5      2      4      5      2      3      2      2      1      1       2

Şimdi veri setinin faktör analizine uygunluğunu inceleyelim. Öncelikli olarak örneklem büyüklüğüne bakalım. Sonrasında korelasyon matrisini oluşturalım ve çoklu bağlantı problemi olup olmadığını “det” fonksiyonu ile test edelim.

nrow(ornek_veri)

## [1] 600

kor.matris<-cor(ornek_veri)

det(kor.matris)

## [1] 0.8437147

Çıktılar incelendiğinde örneklem büyüklüğünün oldukça iyi olduğu (madde başına düşen yanıtlayıcı sayısı 60) görülmektedir. Daha önce değinildiği gibi korelasyon matrisinin determinantının 0.00001’den büyük olması çoklu bağlantı probleminin de bulunmadığını göstermektedir. Şunu hatırlatmakta fayda var ki eğer “Temel Bileşen Analiz” hesaplayacaksanız bu varsayımın karşılanma zorunluluğu yoktur. Ancak diğer faktör analizi yöntemlerinde (faktör çıkarmada kullanılan yöntemler) çoklu bağlantı probleminin karşılanması daha önemlidir (Tabachnik & Fidell, 2013). Analiz çıktısı incelendiğinde (determinant=0.84) veri setinde çoklu bağlantı probleminin olmadığı görülmektedir.

Şimdi KMO örneklem yeterliği ve Bartelet küresellik testi sonuçlarını inceleyelim. Bunun için sırasıyla “kmo” ve “cortest.bartlett” fonksiyonlarından faydalanacağız. Bu fonksiyonlar “psych” paketinde yer almaktadır. Önceki bölümlerde bu analizlerin detaylarına değinilmişti.

library(psych)

KMO(kor.matris)

## Kaiser-Meyer-Olkin factor adequacy
## Call: KMO(r = kor.matris)
## Overall MSA =  0.58
## MSA for each item = 
##  Item.1  Item.2  Item.3  Item.4  Item.5  Item.6  Item.7  Item.8  Item.9 Item.10 
##    0.58    0.56    0.58    0.53    0.50    0.60    0.60    0.56    0.55    0.60

cortest.bartlett(ornek_veri)

## $chisq
## [1] 101.0865
## 
## $p.value
## [1] 3.402261e-06
## 
## $df
## [1] 45

Analiz sonuçlarında hem veri setinin tamamı hem de maddeler bazında KMO değerlerinin 0.50’nin üzerinde olduğu görülmektedir. Aslında bu değerler kabul sınırları arasında olmakla beraber bir ölçme aracının yapı geçerliğinin test edilmesi sürecinde KMO değerinin 0.70 ve üzerinde olması önerilebilir. Bu değerin bir miktar düşük çıkmasının nedeni orijinali 32 madde içeren “SAT12” veri setinin ilk 10 maddesini kullanmamız olabilir. Bartlett testi sonucunun ise istatiksel olarak anlamlı olması da veri setinin faktörleşme için uygun olduğunun bir kanıtı olarak görülebilir.

Veri setinin faktör analizi hesaplamak için uygun oluğuna karar verdikten sonra yapılması gereken faktör çıkarmada kullanılacak tekniğe karar vermektir. Eğitim bilimleri ve sosyal bilimler alanında kullanımı yaygın olduğu için “Temel Bileşen Analizi”ni örneklendireceğimizi daha önce belirtmiştik. Bunun için “psych” paketinde yer alan “principal” fonksiyonundan faydalanacağız.

Faktör çıkarma yöntemine karar verdikten sonra faktör sayısına karar vermek gereklidir. Bu amaçla kullanılabilecek yöntemler önceki kısımlarda açıklanmıştı. Biz faktör sayısına karar verme sürecinde ” Horn’un paralel analiz” yöntemini örneklendireceğiz. Bunun için “hornpa” paketinde yer alan aynı isimli fonksiyondan faydalanacağız. İlk olarak “principal” fonksiyonundan faydalanarak maddelere ilişkin özdeğerleri hesaplayalım.

library(psych)

model1<-principal(kor.matris,nfactors = 10, rotate = "none")

model1$values

##  [1] 1.4592994 1.1984068 1.0701922 1.0067477 0.9653820 0.9489070 0.9159340
##  [8] 0.8477153 0.8143508 0.7730650

“principal” fonksiyonunda ilk argüman olarak daha önce oluşturmuş olduğumuz “kor.matris” isimli korelasyon matrisimizi gireriz. İkinci argüman faktör sayısıdır. Burada faktör sayısına bir sınırlama getirmeden madde sayısını gireriz. Bunun nedeni tüm maddelere ilişkin özdeğerleri çıktıda görebilmektir. Üçüncü argüman olarak rotate = "none" yazarız. Henüz faktör sayısı ve faktörler arasındaki korelasyon düzeyleri belli olmadığı için herhangi bir döndürme işlemi yapmayız. Son olarak analiz sonuçlarını aktardığımız “model1” isimli obje içerisinden model1$values komutu ile maddelere ilişkin özdeğerleri çekeriz.

Sonuçlarda görüldüğü gibi “Kaiser” yöntemine göre özdeğeri 1’den büyük 4 madde bulunmaktadır. Ancak faktör sayısını belirlemeden önce bu değerleri paralel analiz sonucunda elde ettiğimiz özdeğerler ile karşılaştırmamız gerekmektedir.

Aşağıda “hornpa” fonksiyonu ile yansız üretilen örneklemler ile elde edilen özdeğer ortalamaları sunulmuştur.

library(hornpa)

PA<-hornpa(k=10,size=600,reps=500)

## 
##  Parallel Analysis Results  
##  
## Method: pca 
## Number of variables: 10 
## Sample size: 600 
## Number of correlation matrices: 500 
## Percentile: 0.95 
## 
## Compare your observed eigenvalues from your original dataset to the 95 percentile in the table below generated using random data. If your eigenvalue is greater than the percentile indicated (not the mean), you have support to retain that factor/component. 
##  
##  Component  Mean  0.95
##          1 1.206 1.262
##          2 1.144 1.187
##          3 1.095 1.127
##          4 1.053 1.086
##          5 1.014 1.043
##          6 0.977 1.004
##          7 0.940 0.970
##          8 0.901 0.931
##          9 0.859 0.892
##         10 0.810 0.854

PA$Mean

##  [1] 1.206 1.144 1.095 1.053 1.014 0.977 0.940 0.901 0.859 0.810

“hornpa” fonksiyonunda ilk argüman olarak orijinal veri setindeki madde sayısı ikinci argüman olarak orijinal veri setindeki örneklem büyüklüğü girilir. Son argüman ise tekrar sayıdır. Bu sayı yansız (rastgele) olarak kaç simülatif veri setinin üretileceği belirtilir. Biz burada “500” olarak belirledik. Genel olarak 100’ün üzerindeki tekrar sayıları kabul görmektedir.

Akabinde PA$Mean komutu ile üretilen 500 veri setinden elde edilen özdeğerlerin ortalamasını çekeriz. Şimdi faktör sayısına karar vermek için orijinal veriden elde ettiğimiz özdeğerleri paralel analiz sonrasında elde ettiklerimizle karşılaştıralım. Bu işlemi daha anlaşılır hale getirmek için sonucu grafik üzerinde göstermek oldukça faydalı bir yol olacaktır. Aşağıda “plot” fonksiyonu ile oluşturulan ve hem orijinal hem de paralel analiz sonucunda elde edilen özdeğerleri içeren bir yamaç birikinti grafiği sunulmuştur.

    plot(model1$values, type = "b",col=2,lty=1, main = " YAMAÇ GRAFİĞİ VE PARALEL ANALİZ", xlab = "Faktör Sayısı",
      ylab = " Öz Değer")
      lines(PA$Mean,type="b",col=1,lty=2)
      legend("topright", legend=c("PA Ortalama", "Öz Değer"), col=1:2,lty=c(2,1), lwd=2)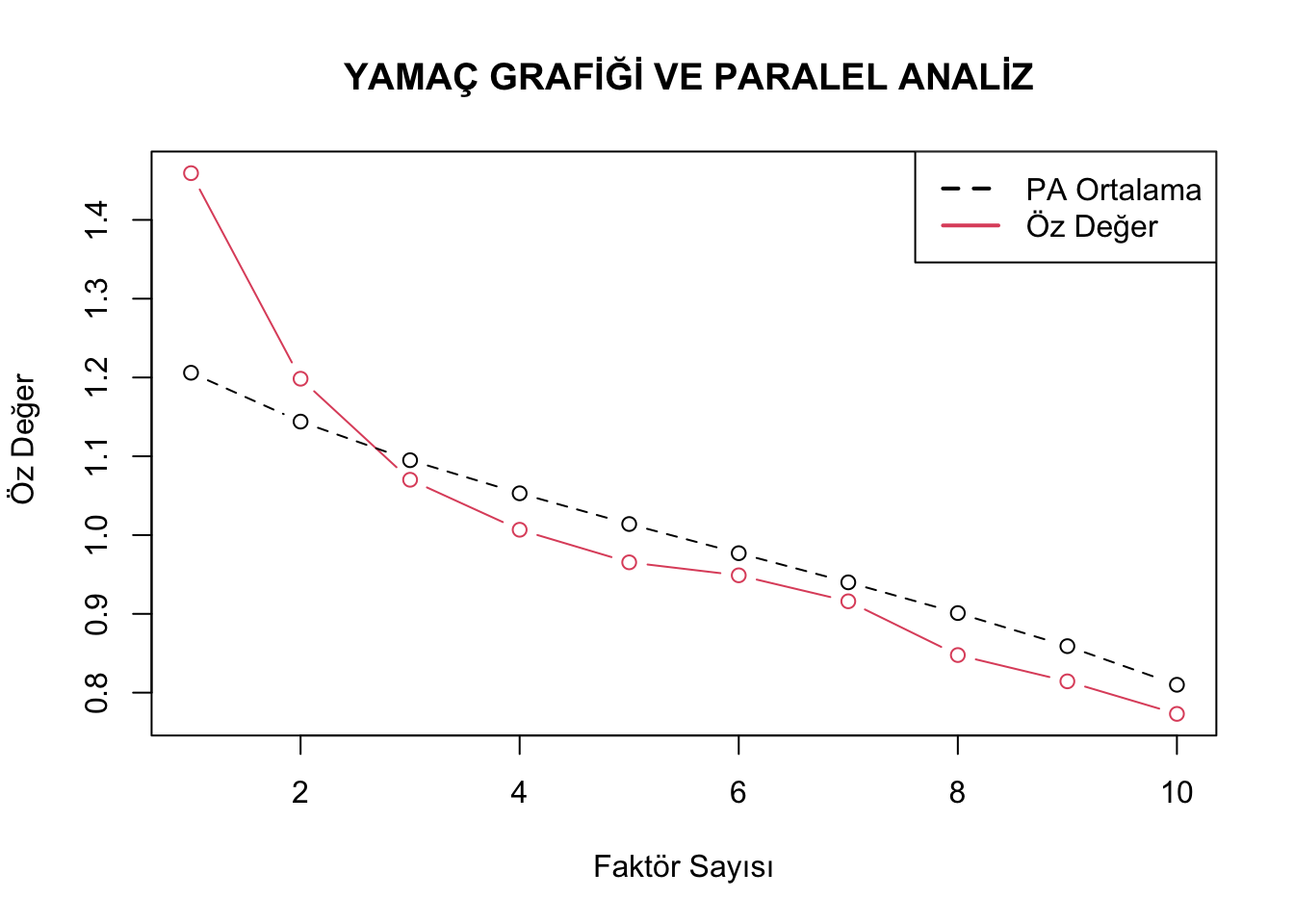

Grafikte kesikli siyah çizgi paralel analiz sonucunda elde edilen özdeğerlerin ortalamasını, düz kırmızı çizgi ise orijinal veriden elde edilen özdeğerleri göstermektedir. Sonuçlara bakıldığında ilk iki faktör için orijinal özdeğerler daha büyük iken 3. faktörden sonra paralel analiz ile elde edilen özdeğeler daha büyüktür. Bu durumda veriyi iki faktörlü olarak kabul etmek doğru olacaktır. Aşağıda iki faktörlü yapı için hangi döndürme yaklaşımının kullanılacağına karar vermek için faktörler arasındaki korelasyonlar sunulmuştur.

model2<-principal(kor.matris,nfactors=2, rotate = "oblimin")

model2$Phi

##            TC1        TC2
## TC1 1.00000000 0.08247755
## TC2 0.08247755 1.00000000

Faktör sayısına karar verdikten sonra döndürme yaklaşımını belirlemek için yine “principal” fonksiyonundan faydalanırız. İlk örneğimizden farklı olarak faktör sayısını iki ile kısıtlarız. Bir diğer farklılık döndürme yöntemidir. Aslında henüz faktörler arasındaki bir ilişki olup olmadığını bilmiyoruz ancak kodlarda görüldüğü gibi döndürme yöntemi olarak eğik döndürme yöntemlerinden “oblimin” belirtilmiştir. Bunun temel nedeni döndürme yöntemini “oblimin” olarak belirlediğimizde faktörler arasındaki korelasyon katsayılarını çıktı olarak bize sunmasıdır. Bu nedenle Palland (2015) faktör analizinde faktörler arası korelasyon sonuçlarını kontrol etmek ve döndürme yöntemine doğru karar vermek için faktör analizine “oblimin” döndürme yöntemi ile başlanmasını önermektedir. model2$Phi komutu ile faktörler arasındaki korelasyon katsayısı sonuçlarını çekebiliriz.

Çıktıda görüldüğü gibi faktörler arasında çok düşük bir korelasyon (0.08) vardır. Yani faktörler bağımsızdır. Bu nedenle dik döndürme yöntemlerinin kullanılması uygun olacaktır. Şimdi döndürme yöntemini dik döndürme yöntemlerinden “varimax” olarak değiştirip aynı işlemi tekrar edelim. sonrasında model$loadings komutu ile döndürme sonrası faktör yüklerini çağıralım.

model3<-principal(kor.matris,nfactors=2, rotate = "varimax")

model3$loadings

## 
## Loadings:
##         RC1    RC2   
## Item.1   0.324  0.535
## Item.2         -0.634
## Item.3  -0.606       
## Item.4          0.124
## Item.5  -0.300  0.282
## Item.6   0.563  0.113
## Item.7   0.439       
## Item.8          0.431
## Item.9  -0.258  0.535
## Item.10  0.488       
## 
##                  RC1   RC2
## SS loadings    1.384 1.274
## Proportion Var 0.138 0.127
## Cumulative Var 0.138 0.266

Çıktıda görüldüğü gibi 4 numaralı madde (Item.4) düşük faktör yük değerine sahip. 5 numaralı madde (Item.5) ise birinci faktörde kabul edilebilecek bir faktör yüküne sahip olmakla birlikte ikinci faktörde de yakın bir yük değerine sahiptir (iki faktör yükü arasındaki fark 0.10’dan daha küçük). Bu nedenle 5 numaralı maddenin hangi faktörde yer aldığı belirgin değildir. Bu noktada bu maddeleri sırası ile çıkarıp analizi tekrar etmemiz gerekmektedir. Öncelikli olarak düşük faktör yüküne sahip 4 numaralı maddeyi çıkarıp analizi tekrarlayalım.

kor.matris1<-cor(ornek_veri[,-4])

model4<-principal(kor.matris1,nfactors=2, rotate = "varimax")

model4$loadings

## 
## Loadings:
##         RC1    RC2   
## Item.1   0.359  0.523
## Item.2  -0.101 -0.639
## Item.3  -0.605       
## Item.5  -0.280  0.301
## Item.6   0.571       
## Item.7   0.441       
## Item.8          0.412
## Item.9  -0.222  0.553
## Item.10  0.490       
## 
##                  RC1   RC2
## SS loadings    1.397 1.256
## Proportion Var 0.155 0.140
## Cumulative Var 0.155 0.295

Çıktıda görüldüğü gibi 4 numaralı madde analiz dışında bırakılsa bile 5 numaralı maddenin hangi faktör altında yer alacağı belirginleşmiyor. Sadece öncesinde birinci faktörde daha yüksek yük değeri verirken şimdi 2. faktörde daha yüksek yük vermeye başlıyor. (Böyle durumlarda alan uzman görüşleri ve değerlendirmeleri önemlidir). Şimdi 4 numaralı maddeyi ölçekte tutarak 5 numaralı maddeyi çıkaralım ve aynı işlemleri tekrar edelim.

kor.matris2<-cor(ornek_veri[,-5])

model5<-principal(kor.matris2,nfactors=2, rotate = "varimax")

model5$loadings

## 
## Loadings:
##         RC1    RC2   
## Item.1   0.308  0.551
## Item.2         -0.660
## Item.3  -0.569       
## Item.4          0.121
## Item.6   0.608       
## Item.7   0.447       
## Item.8          0.441
## Item.9  -0.285  0.554
## Item.10  0.537       
## 
##                  RC1   RC2
## SS loadings    1.361 1.265
## Proportion Var 0.151 0.141
## Cumulative Var 0.151 0.292

Çıktıda görüldüğü gibi sorunlu olan her iki maddeyi de teker teker ölçek dışında bıraktığımızda diğer sorunlu madde de bir düzelme olmuyor. Bu nedenle sorunlu olan her iki maddeyi de ölçek dışında bırakıp analiz sürecini tekrar edelim ve sonuçları yorumlayalım.

kor.matris3<-cor(ornek_veri[,c(-4,-5)])

model6<-principal(kor.matris3,nfactors=2, rotate = "varimax")

model6$loadings

## 
## Loadings:
##         RC1    RC2   
## Item.1   0.332  0.548
## Item.2         -0.668
## Item.3  -0.570       
## Item.6   0.612       
## Item.7   0.448       
## Item.8          0.423
## Item.9  -0.261  0.567
## Item.10  0.537       
## 
##                  RC1   RC2
## SS loadings    1.371 1.250
## Proportion Var 0.171 0.156
## Cumulative Var 0.171 0.328

Analiz sonuçları incelendiğinde toplam 8 maddenin 2 faktör altında toplandığı ve bu iki faktörün toplam varyansın yaklaşık %33’ünü açıkladığı görülmektedir. Birinci faktöre ilişkin öz değer 1.371 iken 2. faktöre ilişkin özdeğer 1.250’dir. Birinci faktör tarafından açıklanan varyans yaklaşık olarak %17 (1.371/8) iken ikinci faktör tarafından açıklanan varyans % 16 civarındadır (1.250 /8). Faktör yükleri incelendiğinde 3, 6, 7, ve 10 numaralı maddelerin 1.faktör altında 1,2,8 ve 9 numaralı maddelerinde 2. faktör altında toplandığı görülmektedir.

AFA hesaplama sürecinde faktör yükleri bize bazı önemli ipuçlarını da verebilirler. Örneğin bir maddenin birden fazla faktörde yüksek düzeyde faktör yüküne sahip olması o maddenin tek boyutlu olmadığını ve iki boyutu da baskın olarak ölçebildiğinin göstergesi olabilir (örneğin soru kökünde uzun bir metin barındıran bir matematik sorusunun hem okuduğunu anlama hem de matematik becerisini ölçmesi gibi). Eğer böyle bir durum ölçekte yer alan pek çok madde de söz konusu ile ölçeğin çok boyutlu yöntemler ile ölçeklenmesi önerilir.